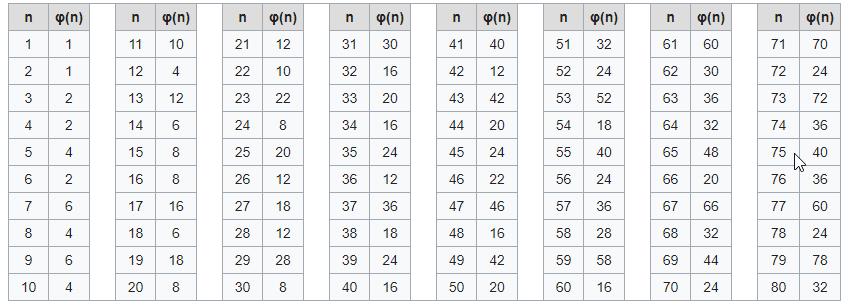
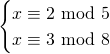Bij een extremumvraagstuk denken we al snel aan het berekenen van de afgeleide functie. Maar sommige extremumproblemen kunnen ook opgelost worden met een methode die geïnspireerd is door de lineaire programmatie. We spreken van niet-lineaire programmatie.
We bespreken een voorbeeld: Bepaal de afmetingen van de rechthoek met maximale oppervlakte waarvan de omtrek constant ( =2a) is.
Noem x en y de afmetingen van de rechthoek. Dan zoeken we naar het maximum van ![]() onder de randvoorwaarden:
onder de randvoorwaarden:
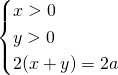
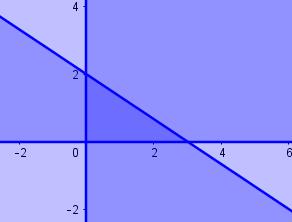
Het ‘gunstig gebied’ is het lijnstuk AB. De niveaulijnen zijn rechthoekige hyperbolen van de vorm ![]() .
.
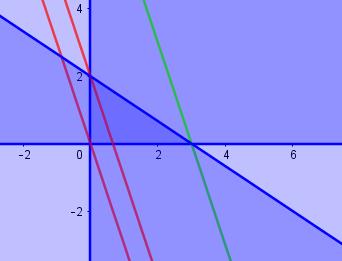
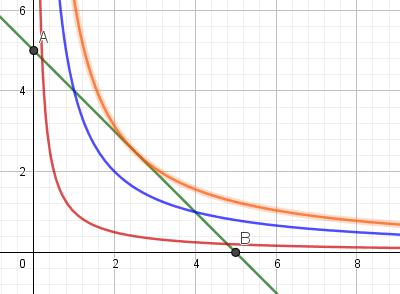 We zien enkele van die hyperbolen getekend, voor
We zien enkele van die hyperbolen getekend, voor ![]() ( rood), voor
( rood), voor ![]() (blauw). We gaan op zoek naar die hyperbool die nog net raakt aan het lijnstuk AB. Daarvoor moet het stelsel :
(blauw). We gaan op zoek naar die hyperbool die nog net raakt aan het lijnstuk AB. Daarvoor moet het stelsel : 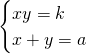 een dubbele oplossing hebben. Met andere woorden de vergelijking
een dubbele oplossing hebben. Met andere woorden de vergelijking ![]() heeft een dubbele oplossing. Hiervoor moet de discriminant nul zijn :
heeft een dubbele oplossing. Hiervoor moet de discriminant nul zijn : ![]() of
of ![]() . Die dubbele wortel is dan
. Die dubbele wortel is dan ![]() . Voor een maximale oppervlakte moeten dus lengte en breedte allebei gelijk zijn aan
. Voor een maximale oppervlakte moeten dus lengte en breedte allebei gelijk zijn aan ![]() .
.




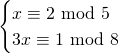 of
of