Categorie archieven: Kansrekenen

De negatieve binomiale verdeling

Geplaatst op door

Bij herhaalde onafhankelijke uitvoeringen van eenzelfde Bernoulli experiment (met succeskans p), kunnen we ook vragen wanneer we juist r keer succes hebben verkregen. Noteer met X de stochast die het tijdstip weergeeft van de r-de succes.

  • X heeft als waarden r,r+1,r+2,…
  • P(X = k) is de kans dat het r-de succes bereikt wordt bij de k-de beurt. Dit is de kans op 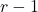r - 1 successen bij de eerste 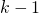k-1 uitvoeringen vermenigvuldigd met de kans op succes bij de k-de uitvoering. Dus

        \[P(X = k)=\binom{r-1}{k-1}p^{r-1}q^{k-r}.p=\binom{r-1}{k-1}p^rq^{k-r}\]

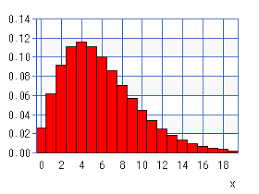
  • Deze verdeling heet de negatieve binomiale verdeling of Pascal verdeling, met parameters r en p.
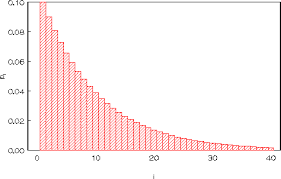
  • Voor r=1 krijgen we uiteraard de geometrische verdeling met parameter p.
  • Het gemiddelde van deze verdeling is E(X)=\frac{r}{p}.
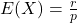  • De berekening van kansen i.v.m. een negatieve binomiale verdeling kan gebeuren met de tabellen van de binomiale verdeling. Noteer met Y de stochast van de binomiale verdeling met parameters k en p, dan geldt

        \[P(X=k)=\frac{r}{k}P(Y=r)\]

De geometrische verdeling

Geplaatst op door

Veronderstel dat we n onafhankelijke uitvoeringen doen van eenzelfde Bernoulli experiment met succeskans p. Bij de binomiaalverdeling stellen we ons de vraag hoeveel keer succes hebben we. Nu stellen we volgende vraag: na hoeveel uitvoeringen boeken we voor het eerst succes?  

Bijvoorbeeld: hoeveel keer moet de gokker roulette spelen om voor het eerst te winnen?

X is het tijdstip van het eerste succes. X is een stochast met waarden 1,2,…

    \[\text{P(X=k)}=q^{k-1}p\]

We zeggen dat X een geometrische verdeling heeft met parameter p. Het is inderdaad een kansverdeling want de som van alle kansen is 1.

Een voorbeeld van een geometrische verdeling met p=0,10:

Het gemiddelde van zo een geometrische verdeling is \frac{1}{p}. Een belangrijke eigenschap van de geometrische verdeling is het geheugenverlies: ze vergeet het verleden. Als we weten dat uitvoeringen 1 tot en met i mislukkingen waren, dan heeft de wachttijd vanaf die i-de mislukking tot het eerste succes, juist dezelfde verdeling als de wachttijd vanaf het begin. Met andere woorden de verdeling van die wachttijd tot het eerste succes hangt helemaal niet af van het aantal mislukkingen dat tot dan toe gebeurd is. In symbolen:

    \[P(X>i+j|X>i)=P(X>j)\]

Andere dobbelstenen

Geplaatst op door

Iedereen kent deze klassieke dobbelsteen. Nemen we nu twee van dergelijke dobbelstenen en berekenen we de som van het aantal ogen: 

De vraag is nu: kunnen we geen ander stel van dobbelstenen vinden die dezelfde verdeling geeft?

  • We stellen onze gewone dobbelsteen voor door

        \[x^6+x^5+x^4+x^3+x^2+x\]

    Je leest deze veelterm als: er is 1 kant met 6stippen, 1 kant met 5 stippen,…
  • Wanneer je nu met 2 dobbelstenen gooit, voer je eigenlijk het product uit van die veelterm met zichzelf en krijg je dus (x^6+x^5+x^4+x^3+x^2+x)^2=x^{12}+2x^{11}+3x^{10}+...+x^2 Je leest in deze uitkomst dan volledig het bovenstaande schema.
  • Noem nu het gezochte stel andere dobbelstenen door f(x) en g(x).
  • We willen dat f(x).g(x)=x^{12}+2x^{11}+3x^{10}+...+x^2 .
  • De ontbonden vorm van de veelterm in het rechterlid is

        \[x^2(x+1)^2(x^2+x+1)^2(x^2-x+1)^2\]

  • Hieruit volgt dat we opzoek moeten naar een a,b,c en d  zodat

        \[f(x)=x^a(x+1)^b(x^2+x+1)^c(x^2-x+1)^d\]


    g(x)=x^{2-a}(x+1)^{2-b}(x^2+x+1)^{2-c}(x^2-x+1)^{2-d}
  • Omdat we zes zijvlakken hebben moet f(1)=6 , dus moet 2^b3^c=6 of b=c=1
  • Verder kan a zeker niet nul zijn want dan zou f(0) niet 0 zijn. En dus kan a ook niet 2 zijn. Bijgevolg is a=1.
  • Voor d=1 krijgen we de klassieke dobbelstenen.
  • Nemen we d=0, dan is f(x)=x(x+1)(x^2+x+1)=x^4+2x^3+2x^2+x. Dis geeft een dobbelsteen met op de zijvlakken 4/3/3/2/2/1
  • De andere dobbelsteen geeft dat g(x)=x(x+1)(x^2+x+1)(x^2-x+1)^2=x^8+x^6+x^5+x^4+x^3+x of een dobbelsteen met op de zijvlakken 8/6/5/4/3/1.
  • Hier zie je dat de verdeling inderdaad hetzelfde is tussen de 2 sets van dobbelstenen.

 

Verwachtingswaarde

Geplaatst op door

Hoeveel keer moet je gemiddeld een eerlijk muntstuk opgooien om 5 keer na elkaar kop te krijgen?

Antwoord

  • Noteer met e de gezochte verwachtingswaarde van het aantal keer opgooien. We noteren K voor kop en M voor munt.
  • Stel dat je bij de eerste poging M gooit. Hiervoor heb je \frac{1}{2} kans. Dan heb je nog steeds geen enkele keer K gehad en dus moet je gemiddeld nog e+1 keer opgooien voordat je er bent. Die 1 komt van de poging die je al hebt ondernomen.
  • Heb je eerst K en dan M, en daartoe heb je \frac{1}{4} kans, dan moet je weer van vooraf aan beginnen en heb je gemiddeld e+2 pogingen nodig. De 2 staat er omdat je al 2 keer gegooid hebt( KM) en dan helemaal opnieuw moet beginnen. 
  • Werk zo verder de gevallen KKM ,KKKM,KKKKM en KKKKK af
  • Ga zo verder en dan krijg je volgende vergelijking :
    e=\frac{1}{2}(e+1)+\frac{1}{4}(e+2)+\frac{1}{8}(e+3)+\frac{1}{16}(e+4)+ \frac{1}{32}(e+5)+\frac{1}{32}.5
  • Oplossen van deze vergelijking geeft e=62.

Even en oneven elementen

Geplaatst op door

Hoe groot is de kans dat bij een permutatie van \{1,2,...,n\} geen 2 even elementen en geen 2 oneven elementen naast elkaar staan?

Of anders geformuleerd: Er zijn in een gezelschap een aantal jongens en een aantal meisjes. Ze moeten op 1 rij gaan staan. Hoe groot is de kans dat geen twee jongens of twee meisjes naast elkaar gaan staan?

  • Het totaal aantal permutaties van n elementen is n!.
  • Als n even is ( n = 2m) zijn er evenveel jongens als meisjes. Er zijn twee mogelijke schikkingen JMJM… of MJMJ…; Bij elk van de mogelijkheden kan je de jongens op m! manieren ordenen en ook de meisjes op m! manieren rangschikken. Het totaal aantal mogelijkheden is dus 2.m!.m!
  • Als n oneven is (n = 2m – 1) zijn er bijvoorbeeld m – 1 jongens en m meisjes. in dit geval kan je enkel MJM…krijgen en zijn er dus in het totaal (m-1)!.m! mogelijkheden.
  • Noteer met P(n) de kans dat geen twee jongens of twee meisjes naast elkaar gaan staan bij n personen. Als n = 2m, dan is

        \[K(2m)=K(2m-1)=\frac{m!}{m(m+1)...(2m-1)}\]

  • Zo is K(1)=K(2)=1; K(3)=K(4)=33,3% ; K(5)=K(6)=10% ; K(7)=K(8)=2,86% en K(9)=K(10)=0,79%