Bepaal het aantal oneven binomiaalgetallen in 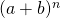 .
.
Antwoord
- Een binomiaalgetal is van de vorm:
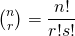 met
met 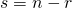 .
. - We noteren de getallen n,r en s in het binair talstelsel:
![Rendered by QuickLaTeX.com \[n=\sum_{i=0}^hn_i.2^{h-i}\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-0a461b163b130555b12f5672bfe5a547_l3.png)
![Rendered by QuickLaTeX.com \[r=\sum_ir_i.2^{k-i}\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-94416626356e5f4fc61a4c18bfaac569_l3.png)
![Rendered by QuickLaTeX.com \[s=\sum_i^ps_i.2^{p-i}\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-ba1bb5df96b961585aeab0256809b2c5_l3.png)
met
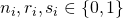 en
en 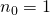
- De exponent van 2 in n! is gelijk aan
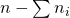 . De exponent van 2 in r! is gelijk aan
. De exponent van 2 in r! is gelijk aan 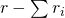 . De exponent van 2 in s! is gelijk aan
. De exponent van 2 in s! is gelijk aan 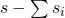 .
.
Voor meer uitleg lees volgend artikel - Als het binomiaalgetal oneven moet zijn, dan mag
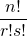 geen factor 2 meer bevatten en moet dus
geen factor 2 meer bevatten en moet dus 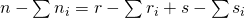 .
. - Bijgevolg is
 oneven als
oneven als  .
. - Het aantal oneven binomiaalgetallen komt dus overeen met het aantal keuzes van r, tussen 0 to n , waarvoor
 .
. - Als
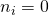 moet
moet 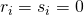 . Er is dus
. Er is dus 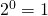 mogelijkheid
mogelijkheid - Als
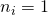 , dan heb je
, dan heb je 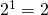 mogelijkheden:
mogelijkheden: 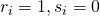 of
of 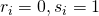 .
. - Noteer
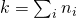 , dan zijn er dus
, dan zijn er dus 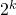 oneven binomiaalgetallen.
oneven binomiaalgetallen. - Er zijn dus
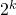 oneven binomiaalgetallen in
oneven binomiaalgetallen in 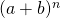 , waarbij
, waarbij 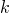 gelijk is aan de som van de cijfers in de binaire schrijfwijze van
gelijk is aan de som van de cijfers in de binaire schrijfwijze van 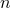 .
. - Controleer met een voorbeeld : voor
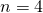 heb je als binomiaalgetallen: 1,4,6,4,1. Er zijn dus 2 oneven binomiaalgetallen. Nu is 4 = 100 in het binair talstelsel en dus is
heb je als binomiaalgetallen: 1,4,6,4,1. Er zijn dus 2 oneven binomiaalgetallen. Nu is 4 = 100 in het binair talstelsel en dus is 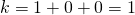 . Er zijn dus
. Er zijn dus 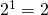 oneven binomiaalgetallen.
oneven binomiaalgetallen.
