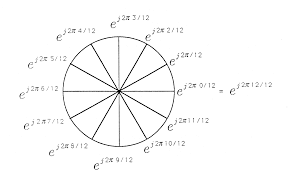
Noteer alle niet-triviale n-de machtswortels uit 1 door ![]() . Stel
. Stel ![]() . Vorm nu de uitdrukkingen
. Vorm nu de uitdrukkingen ![]() en bewijs dat
en bewijs dat
![]()
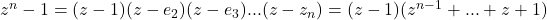
- Dus is
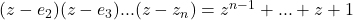
- Stel hierin
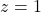 en je vindt dat het rechterlid uit de te bewijzen formule gelijk is aan
en je vindt dat het rechterlid uit de te bewijzen formule gelijk is aan 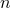 .
. - Verder is het linkerlid gegeven door
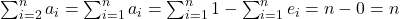 .
. - Bij de laatste stap maken we gebruik van de eigenschap dat de som van de wortels van
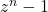 gelijk is aan de coëfficiënt van de op één na hoogste graadsterm.
gelijk is aan de coëfficiënt van de op één na hoogste graadsterm. - Hiermee is het gestelde bewezen.