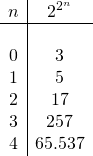Tag archieven: euler

De ongelijkheid van Euler

Geplaatst op door

Eén van de oudste ongelijkheden in een driehoek is de ongelijkheid van Euler die een verband geeft tussen de stralen van de omgeschreven en ingeschreven cirkel.

Als O het middelpunt is van de omgeschreven cirkel ( met straal R) van driehoek ABC en I het middelpunt van de ingeschreven cirkel (met straal r), noteer dan d=|OI|. Dan geldt er:

    \[d^2=R^2-2Rr\]

Hieruit volgt dan dat

    \[R\geq 2r\]

Het gelijkheidsteken geldt enkel als de driehoek gelijkzijdig is.

Fermat priemgetallen en regelmatige veelhoeken

Geplaatst op door

De Franse wiskundige Pierre de Fermat( 1601-1665) dacht dat alle getallen van de vorm 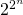2^{2^n} priemgetallen waren. En voor de eerste 5 waarden van n was dat ook zo:

\begin{array}{c|c} n& 2^{2^n} \\ \hline\\ 0 &3\\1&5\\2&17\\3&257\\4&65.537\end{array}

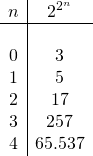
Later ontdekte Leonard Euler( 1707-1783) in 1732 dat het Fermat getal voor n = 5 ontbonden kon worden als  4.294.967.297 = 641 x 6.700.417. En hier zou het verhaal dan stoppen, ware er niet de geniale ontdekking van Carl Friedrich Gauss(1777-1855).

In 1794 vond Gauss dat een regelmatige veelhoek met p zijden (met p een priemgetal ) construeerbaar is met passer en liniaal als en slechts als p een Fermat priemgetal is, dus een priemgetal van de vorm 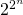2^{2^n}. Als eerbetoon werd in Brauschweig, de thuisstad van Gauss,  een bronzen standbeeld opgericht waar hij staat op een regelmatige zeventien hoek.

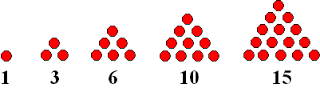
Welke regelmatige veelhoeken zijn dan construeerbaar met passer en liniaal? Volgens Gauss’ resultaat zijn dat de gelijkzijdige driehoek, de regelmatige 5-hoek, de regelmatige 17-hoek, de regelmatige 257-hoek en de  regelmatige 65.537-hoek. We weten dat ook de regelmatige veelhoeken met 7,11,13,19,… zijden niet construeerbaar zijn omdat het wel priemen zijn, maar geen Fermat priemen. Verder zijn ook regelmatige veelhoeken met 4,8,16,32,.. en 6,12,24,48,… zijden construeerbaar omdat we met passer en liniaal een hoek in twee kunnen verdelen. En wat met de anderen? Is een regelmatige 15 hoek construeerbaar?  Het blijkt van wel, omdat 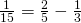\frac{1}{15}=\frac{2}{5}-\frac{1}{3} en dus kunnen we een cirkel in 15 gelijke delen verdelen.

Het was uiteindelijk Pierre Wantzel die in 1837 volgend algemeen reultaat bewees: Een regelmatige n-hoek is construeerbaar met passer en liniaal als en slechts als n het product is van een macht van 2 en een willekeurig aantal verschillende Fermat priemgetallen.

De kleine stelling van Fermat

Geplaatst op door

Als p een priemgetal is en a en p onderling ondeelbaar zijn dan geldt:

    \[a^{p-1} \equiv 1 \text{ mod } p\]

Uit deze stelling, die de kleine stelling van Fermat genoemd wordt en in 1640 een eerste keer vermeld werd, volgt dat voor elke a en voor een priemgetal p geldt dat

    \[a^p \equiv a \text { mod } p\]

De stelling wordt bijvoorbeeld gebruikt om de restklasse modulo een groot getal uit te rekenen. Bereken bijvoorbeeld de rest bij deling van 2^{245} door 11. Volgens de kleine stelling van Fermat is 2^{10} \equiv 1 \text{ mod } 11, dus is 2^{245} \equiv (2^{10})^24.2^5 \equiv 2^5 \equiv 10 \text{ mod } 11.

Er bestaat een veralgemening voor de stelling, die zegt dat als a en m onderling ondeelbaar zijn, geldt

    \[a^{\varphi(m)} \equiv 1 \text { mod }m\]

Hierbij is \varphi(m) de totiënt functie van Euler die het aantal getallen, kleiner dan m, berekent die onderling ondeelbaar zijn met m. Deze stelling wordt de Euler-Fermat stelling genoemd.

Opgave 1: Driehoeksgetallen

Geplaatst op door

driehoeksgetallen

Hierboven zie je de eerste 5 driehoeksgetallen. Kan je nu de volgende vragen beantwoorden?

  1. Als n een driehoeksgetal is, bewijs dan dan 8n+1 een volkomen kwadraat is.
    ( Plutarchus , 100 BC)
  2. De som van twee opeenvolgende driehoeksgetallen is altijd een volkomen kwadraat. Bewijs. ( Nicomachus, 100 BC)
  3. Als n een driehoeksgetal is, bewijs dan dat 9n+1 en 25n+3 ook driehoeksgetallen zijn. ( Euler, 1775)

Antwoorden Vraag 1
Een driehoeksgetal is de som van opeenvolgende natuurlijke getallen, beginnend met 1. Dus het n-de driehoeksgetal d_n wordt gegeven door d_n=1+2+3+...+n=\dfrac{n(n+1)}{2}. Maar dan is 8d_n+1=4n(n+1)+1=4n^2+4n+1=(2n+1)^2. Bijgevolg is 8d_n+1 een volkomen kwadraat.

Antwoorden Vraag 2
Gebruikmakend van vorige formule is d_n+d_{n+1}=\dfrac{n(n+1)}{2}+\dfrac{(n+1)(n+2)}{2}=\dfrac{n^2+n+n^2+3n+2}{2}. Dus is d_n+d_{n+1}=n^2+2n+1=(n+1)^2. De som van twee opeenvolgende driehoeksgetallen is dus inderdaad een volkomen kwadraat.

Antwoorden Vraag 3
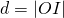Stel d_n=\dfrac{n(n+1)}{2}. Dan is 9d_n+1=\dfrac{9n(n+1)}{2}+1=\dfrac{9n^2+9n+2}{2}. Dus 9d_n+1=\dfrac{(3n+1)(3n+2)}{2}=d_{3n+1}. Analoog is 25d_n+3=d_{5n+2}.