Tag archieven: Griekse wiskunde

Griekse wiskunde : deel 9

Geplaatst op door

Na Apollonius begint voor de Griekse meetkunde een periode van stagnatie en verval. Personen zoals Heron van Alexandrië (1ste eeuw NC), Menelaos van Alexandrië(1ste eeuw NC), Theon van Alexandrië(4e eeuw NC), Proclus en Pappus leveren weinig nieuwe bijdragen , maar brengen hoofdzakelijk commentaren op en aanvullingen van de werken van de oude meesters. De laatste Alexandrijnse wiskundige is Hypatia, de eerste bekende vrouwelijke wiskundige.

De voornaamste redenen van de teleurgang van de Griekse meetkunde zijn:

  • Het gebrek aan belangstelling van de Romeinse keizers voor de zuivere wetenschappen.
  • De uitbuiting van de Hellenistische landen door de Romeinen, waardoor het wetenschappelijk onderzoek niet langer financieel gesteund werd.
  • Het ontbreken van zuiver-algebraïsche methodes ( en vooral symbolen) waardoor een verdere ontwikkeling bemoeilijkt wordt.

Griekse wiskunde deel 7

Geplaatst op door

Archimedes leefde in Syracuse van 287 tot. 212 v.C. en verbleef aan het hof van koning Hieron. Bij zijn tijdgenoten verwierf hij grote vermaardheid, niet zozeer voor zijn zuiver wetenschappelijk werk, maar vooral door zijn talrijke technische realisaties van ingenieuze werktuigen en machines( pompen, kranen , katapulten,..).

Als zuiver platonische wiskundige is hij zelf minder gelukkig met zijn materialistische nevenactiviteiten. Tijdens een reis naar Egypte maakt hij kennis met Euclides en vanaf dan onderhoudt hij een vrij drukke wetenschappelijke briefwisseling met andere wiskundigen zoals bvb. Erastosthenes. Meestal deelt hij enkel resultaten mee, daarmee zijn collega’s uitdagend om er zelf een bewijs voor te vinden.

Van zijn uitgebreid oeuvre bleven enkel volgende werken bewaard: Over het evenwicht van vlakke figuren en hun zwaartepunt,  de kwadratuur van de parabool, de methode, over de bol en de cilinder, over de conoïden en de sferoïden. over de spiralen, over de drijvende lichamen, de cirkelmeting en de zandrekenaar.

De methode: dit werk werd pas in 1906 bij toeval teruggevonden door de Deense filoloog Heiberg op een palimpsest uit een kloosterbibliotheek. In dit werk leert Archimedes ons dat de strenge deductieve methode , waarvan Aristoteles de formele regels vastlegde en die Euclides in zijn Elementen zo perfect illustreerde, een procédé is dat haast alleen nuttig is om bewijzen van gekende resultaten te leveren.Voor het creatief onderzoekingswerk geeft hij de voorkeur aan zogenaamde mechanische methodes die, omdat ze op fysische inzichten berusten, minder streng maar zoveel vruchtbaarder zijn. Nadat hij langs deze heuristische weg resultaten ontdekt heeft, geeft hij een streng bewijs waarbij hij dikwijls gebruik maakt van Eudoxos’ exhaustiemethode.

Griekse wiskunde deel 6

Geplaatst op door

Over de mens Euclides is weinig bekend, We weten dat hij rond 300 v.C. wiskunde doceerde in het museion van Alexandrië. Gevormd in de scholen van Plato en Aristoteles, is hij dus één van de Griekse intellectuelen die naar Alexandrië toestroomden om er beroepsgeleerde te worden. 

Uit de analyse van zijn werken is vrij duidelijk te zien dat Euclides geen groot wiskundige was, maar wel een buitengewone didacticus. Zo ligt het geniale van zijn Elementen niet zozeer in de inhoud, want die is afkomstig van zijn grote voorgangers Archytas, Theatetus en Eudoxos. Maar het bijzondere is de gepaste keuze van de volgorde, waar de verschillende onderdelen worden behandeld. Een vrij omvangrijk eerste deel is ook toegankelijk voor middelmatige leerlingen, de moeilijke delen komen pas later aan de beurt.

De elementen staat zeker op de lijst van de boeken die het grootst aantal uitgaven en vertalingen hebben gekend. Deze bestseller omvat 13 boeken, waaraan door latere wiskundigen nog 2 boeken zijn toegevoegd. ( o.a. een boek over regelmatige veelvlakken). De boeken 1 tot 4 handelen over de meetkunde van de rechte, de driehoek en de cirkel. Boeken 5 en 6 zijn gewijd aan de leer van de evenredigheden en de gelijkvormige figuren. In boeken 7,8 en 9 gaat het over de natuurlijke getallen. Boek 10 bestudeert de irrationale getallen. Tenslotte gaat het in de boeken 11,12 en 13 over de meetkunde van de ruimte en de 5 regelmatige veelvlakken.

Griekse wiskunde: deel 5

Geplaatst op door

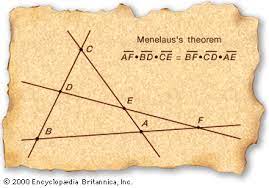
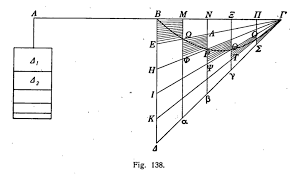
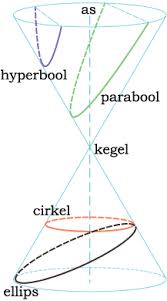
De Hellenistische periode ( 4de -1ste eeuw v.C.) was  het tijdperk waarin het oude Griekenland op zijn hoogtepunt was vanaf de veroveringen door Alexander de Grote tot de Romeinse verovering van Griekenland en het oude Nabije Oosten (334–30 v.Chr.).

De Griekse cultuur verspreidt zich over alle oosterse landen, verrijkt zich aan de Egyptische en Babylonische beschavingen, bereikt nieuwe toppen en deint dan langzaam uit. De nieuwe centra van deze Hellenistische cultuur worden Alexandrië, Seleucia en Syracuse.

De oude schrijfwijze van de getallen ( die van de zelfde aard was als de latere Romeinse) wordt in de derde eeuw v.C. vervangen door een systeem van lettergetallen, dat van Fenicische oorsprong is. De gebruikte tekens zijn de 24 letters van het klassiek-Griekse alfabet, aangevuld met drie oude letters: digamma, koppa en sampi.

De letters worden gevolgd door een accent opdat men ze niet zou verwarren met de letters die woorden vormen. Om duizendtallen aan te duiden plaatst men een accent onderaan links van de letter, die het aantal duizendtallen aangeeft.

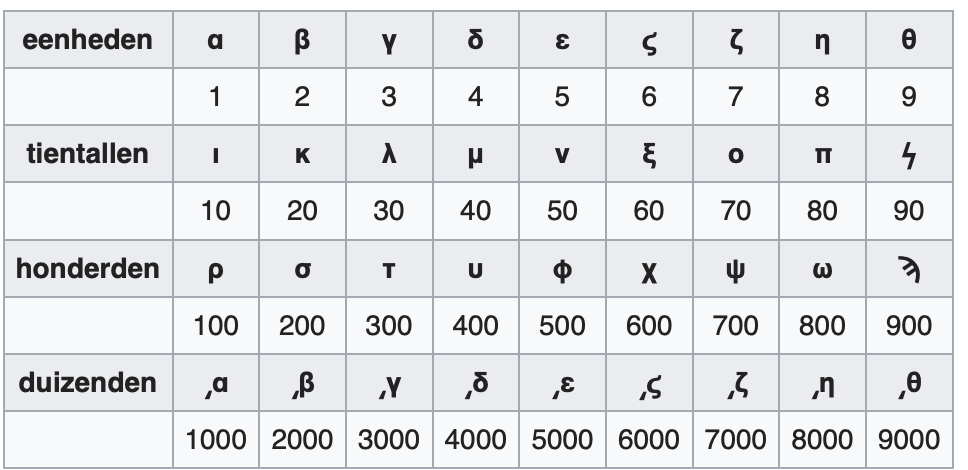
Om ook getallen groter dan 10000 te kunnen schrijven, stelt Appolonius  voor de letter M te plaatsen na de tekens die het aantal tienduizendtallen aanduiden. Zo kunnen uiteindelijk alle getallen tot 99999999 worden voorgesteld. Nochtans steekt de complexiteit van deze vernieuwde Griekse schrijfwijze schril af tegen de eenvoud van het bijna positionele stelsel van de Babyloniërs.

De voorstelling van de breuken is zo mogelijk nog ingewikkelder: enerzijds worden de stambreuken zoals 1/3, 1/4,..; aangeduid met de lettertekens voor 3,4,.. gevolgd door een dubbel accent; anderzijds noteert men een gewone breuk zoals 5/7  met behulp van een streep boven het noemer gedeelte. Deze streep is misschien wel de voorloper van onze breukstreep, zoals ze later door de Arabieren wordt ingevoerd.

De romeinse veroveraars nemen uiteindelijk deze Griekse schrijfwijze niet over.

 

Griekse wiskunde: deel 4

Geplaatst op door

De  4de eeuw voor  Christus: bloeiperiode van de wiskunde. De tijd van Plato en Aristoteles.

We beperken ons tot een overzichtelijke samenvatting van de wiskundige werken, waaruit de krachtlijnen van de onderzoeken zouden moeten blijken. De meeste bijdragen halen een hoog wetenschappelijk niveau en de bewijzen zijn niet alleen wiskundig streng maar getuigen ook van een grote denkkracht en een rijke creativiteit. In het filosofisch stelsel van Plato wordt de wiskunde verheven tot de kunst van het exact redeneren over louter abstracte begrippen, die dus los dienen te staan van elke zintuigelijke waarneming.

  • de  irrationale getallen: Theaetetus (414-370 v.C.), vriend van Plato en Socrates,  stelt in een samenspel tussen meetkunde en getallenleer een classificatie op van 13 irrationaliteiten en bewees ook dat de verzameling irrationale getallen oneindig is.
  • de bekende wiskundige van deze tijd was Eudoxos van Cnidus (405-315 v.C.) .  Hij werkte vooral rond de gulden snede, de doorsnede van krommen en de verdubbeling van een kubus .Hij heeft eveneens ontdekt dat de verhouding van het volume van een piramide ten opzichte van een prisma op hetzelfde grondvlak een op drie is. 
  • De exhaustie methode : het geniale antwoord van Eudoxos op de paradoxen van Zeno. Heeft me, 2 ongelijke grootheden van een zelfde soort, dan kan steeds een natuurlijk getal gevonden worden dat met hun verschil vermenigvuldigd, elke gegeven grootheid van die soort overtreft. Hiermee bewees hij bvb. dat de oppervlakten van twee cirkels zich verhouden als de kwadraten van hun stralen.
  • De 5 regelmatige veelvlakken ( platonische lichamen) , veelvlakken die begrensd zijn door een aantal congruente regelmatige veelhoeken: tetraëder, kubus, dodecaëder, octaëder en de isocaëder. De drie eersten waren reeds bekend aan de Pythagoreeërs. Het was Theaetetus die de laatste twee ontdekte en een nauwkeurige beschrijving gaf van de constructie en de berekening van de ribben in functie van de straal van de omgeschreven bol.
  • Het bestuderen van de 3 grote problemen ( driedeling hoek, verdubbeling kubus en kwadratuur van de cirkel) leidde tot de studie van speciale krommen: de kwadratix ( Hippias van Elis , rond 420 v.C.), de kegelsneden ( Menaechmus rond 350 v.C.)
  • Er ontstond meer en meer de noodzaak om de volledige wiskundige kennis te ordenen tot een samenhangend geheel. Hippochrates van Chios zou de samensteller zijn van de eerste zogenaamde Elementen.  Van hem zijn ook  de maantjes van Hippocrates.