Bewijzen met verhaaltjes

Geplaatst op 12 mei 2020 door admin

Hoe bewijs je volgende formule?

$k(k-1)\binom{n}{k}=n(n-1)\binom{n-2}{k-2}$

Het gaat zeer snel door gebruik te maken van de definitie van binomiaalcoëfficiënten. Maar er is ook een andere manier, die je ook kan gebruiken als het gebruik van de definitie wat ingewikkelder ligt. We verzinnen gewoon een verhaaltje …

Je wilt op school met n leerlingen een leerlingenraad van k personen oprichten, waarbij een voorzitter en een ondervoorzitter moeten aangeduid worden.

Het linkerlid van bovenstaande vergelijking komt overeen met volgende procedure: kies eerst k leden uit de n leerlingen. Dit kan op 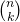$\binom{n}{k}$ manieren. Kies in die groep van k gekozenen een voorzitter ( k mogelijkheden) en een ondervoorzitter ( k-1 mogelijkheden).
Het rechterlid correspondeert met de procedure: kies uit de n leerlingen eerst een voorzitter ( n mogelijkheden), dan een ondervoorzitter( n-1 mogelijkheden) en vul tenslotte aan tot je een groep van k leden hebt. Je moet dus nog k-2 leerlingen kiezen uit de n-2 beschikbare ( 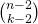$\binom{n-2}{k-2}$ mogelijkheden).
Aangezien beide procedures hetzelfde probleem oplossen , zijn linkerlid en rechterlid gelijk aan elkaar.

Waag eens een gokje

Geplaatst op 15 december 2017 door admin

Je kan een aantal mogelijke oplossingen uitproberen. Misschien kan je zelfs het aantal mogelijke oplossingen beperken. Dan kan je best een gokje wagen en daarna proberen te bewijzen dat jouw voorstel tot oplossing de goede is.

Bepaal de volgende term in de rij:

$-1,-1,1,5,11,19,29,\cdots$

Het is zeker geen rekenkundige rij. Een eerste graadsveelterm zal dus niet kunnen om de algemene term van de rij te bepalen. Het is ook geen meetkundige rij , dus ook een exponentiële functie zal niet volstaan.
Proberen we even met een tweedegraadsfunctie. Dus een uitdrukking van de vorm $P(x)=ax^2+bx+c$ . Proberen we nu de waarden van de onbekenden $a,b$ en $c$ te vinden.
Uit $P(1)=P(2)=-1$ en $P(3)=1$ vinden we een stelsel:
$\left\{ \begin{array}{l}a+b+c=-1 \\ 4a+2b+c=-1\\9a+3b+c=1 \end{array} \right$

.
De oplossing van het stelsel is $a=1$ , $b=-3$ e, $c=1$ .
De vraag is natuurlijk of onze gok goed was! Voldoen de andere termen van de rij ook aan het voorschrift?
Nu is: $P(4)=5$ , $P(5)=11$ , $P(6)=19$ , $P(7)=29$ .
De volgende term in de rij is $P(8)=41$ .

Vereenvoudig

Geplaatst op 15 december 2017 door admin

Als een probleem te moeilijk is om op te lossen, kan het oplossen van een ander, eenvoudiger probleem, dikwijls inspiratie geven om het oorspronkelijk probleem op te lossen. We kunnen bijvoorbeeld eerst speciale gevallen bestuderen of we kunnen bijvoorbeeld één van de voorwaarden weglaten. Of we kunnen concrete gevallen van het algemeen probleem proberen aan te pakken.

Gegeven is een willekeurige driehoek. Construeer een vierkant zodat alle hoekpunten van dat vierkant op de zijden van de driehoek liggen. Twee van de hoekpunten zijn dus gelegen op dezelfde zijde van de driehoek.

We laten één van de voorwaarden weg en proberen eerst een vierkant EDGF te construeren waarvan 2 punten op een zijde van de driehoek liggen en waarvan één ander hoekpunt op een andere zijde van de driehoek ligt.
We gaan het vierkant vergroten zodat D op $[AB]$ blijft en E en F ook op $[A,C]$ blijven. Ondertussen zorgen we ervoor dat G op de derde zijde van de driehoek komt te liggen.We gebruiken hiervoor een homothetie met centrum A die G afbeeldt op H ( het snijpunt van AG met BC).
Het homothetisch beeld van EDGF is dan JIHK en dit vierkant vodoet aan de gestelde voorwaarden.

Kleuringen

Geplaatst op 9 augustus 2017 door admin

Soms kan het nuttig zijn om een rooster in te kleuren en daardoor te bewijzen dat een bepaalde situatie al dan niet mogelijk is. Deze heuristiek wordt dikwijls gebruikt wanneer je een schaakbord moet opvullen met bepaalde vormen.

Voorbeeld: Kan een 10 x 10 schaakbord opgevuld worden met 25 tetrominos van de vorm

Oplossing:

Geef elk vakje van het schaakbord een uniek adres door het rijnummer en kolomnummer van het vakje te noteren. Zo een adres is dan van de vorm $(i,j) \text{ waarbij } 1 \leq i,j \leq 10$ .
Kleur $(i , j )$ met de kleur $t = i +j \text{ mod4 }$ zodat $t \in \{1,2,3,4\}$ . Hierbij is1 = blauw; 2 = geel; 3 = rood; 4 = groen.
Elke tetromino zal door de schikking van de kleuren (cijfers) precies 4 vakjes met vier verschillende kleuren bedekken.
Aangezien er op het bord 25 keer blauw (1), 26 keer geel (2) 25 keer rood (3) en 24 keer groen (4) voorkomt zal het niet mogelijk zijn om het bord te vullen met 25 tetromino’s

Heuristiek : Blikwissel

Geplaatst op 11 november 2016 door admin

Door onze wiskundige ervaring beperken we ons soms tot die oplossingsmethoden die in het verleden steeds gewerkt hebben. Daardoor zie je soms een eenvoudige uitkomst over het hoofd. Een belangrijke heuristiek is bijgevolg: het probleem op een andere manier bekijken. We noemen dit blikwissel.

We doen alsof we de oplossing hebben en werken zo terug tot we terechtkomen bij een situatie die we wel meester zijn. We proberen een omgekeerde redenering op te zetten door van achter naar voor werken. We leven ons in in de personen, dieren, zaken die in de vraag voorkomen en bekijken het probleem eens vanuit hun standpunt. We kijken naar andere dingen, die niet rechtstreeks gevraagd zijn. We vragen ons af wat de voorlaatste stap van de oplossing zou kunnen zijn.

Bekijken we volgend voorbeeld:

Je beschikt over twee emmers, één van 9 liter en een van 4 liter. Hoe kan je hiermee precies 6 liter water uit een waterput afmeten?

We vragen ons af wat de voorlaatste stap van de oplossing zou kunnen zijn. Om 6 liter in de emmer van 9 liter over te houden, willen we die helemaal vullen en er 3 liter uit wegnemen. Dit lukt als we in de kleine emmer 1 liter water hebben staan. Hoe kunnen we nu 1 liter maken met deze twee emmers? Nu is $1=9-4-4$ . Onze strategie is dus:

Vul de grote emmer.
Vul hiermee de kleine emmer en ledig die. Je hebt dus 4 liter uit de grote emmer weggegoten.
Giet nogmaals 4 liter van de grote emmer in de kleine en ledig die weer.
Giet de overblijvende liter in de kleine emmer.
Vul de grote emmer met 9 liter.
Giet van de grote emmer zoveel water over tot de kleine emmer helemaal gevuld is.
Nu blijft er 6 liter over in de grote emmer.

Wiskunde is leuk

Tag archieven: Heuristiek