Hoeveel vierkanten en rechthoeken kan men vormen op een n x n schaakbord?
- Nemen we eerst het aantal vierkanten. We noteren V(n) voor het aantal vierkanten dat je kan tekenen op een nxn bord. Voor de 1×1 vierkanten heb je n mogelijke verticale posities en n horizontale, dus
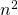 mogelijke vierkanten. Voor de 2×2 vierkanten heb je n – 1 verticale en horizontale mogelijke plaatsingen , dus
mogelijke vierkanten. Voor de 2×2 vierkanten heb je n – 1 verticale en horizontale mogelijke plaatsingen , dus 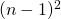 mogelijkheden. Uiteindelijk is het totaal aantal vierkanten gelijk aan
mogelijkheden. Uiteindelijk is het totaal aantal vierkanten gelijk aan 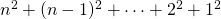 .
.
![Rendered by QuickLaTeX.com \[V(n)=\frac{n(n+1)(2n+1)}{6}\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-32e85565ddcc0bff2e5a6bf3a6479cb7_l3.png)
- Met R(n) noteren we het aantal rechthoeken dat je kant tekenen op een nxn schaakbord. Voor een rechthoek heb je 2 verticale en twee horizontale lijnen nodig. Er zijn n+1 verticale en n+1 horizontale lijnen op een schaakbord. Om de verticale lijnen te kiezen heb je dus
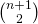
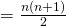 mogelijkheden. Idem voor de keuze van de twee horizontale lijnen. Dus
mogelijkheden. Idem voor de keuze van de twee horizontale lijnen. Dus
![Rendered by QuickLaTeX.com \[R(n)=\frac{n^2(n+1)^2}{4}\]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-a1c467389dd4ad5964117cdbbcd47211_l3.png)
- Voor een 8×8 schaakbord heb je dus 204 vierkanten en 1296 rechthoeken. Van die rechthoeken zijn er 1092 die geen vierkant zijn.

