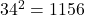Tag archieven: ontbinden in factoren

Nootje 45

Geplaatst op door

Zoek een getal van 4 cijfers, waarbij elk cijfer kleiner is dan 7. Het getal is een kwadraat en als je bij elk cijfer 3 optelt bekom je opnieuw  een getal dat een kwadraat is.

Antwoord

  • Noteer met x het gezochte getal. 
  • Dan kan je schrijven dat 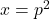x=p^2 met p tussen 31 en 100.
  • Elk cijfer mer 3 vermeerderen betekent dat je 3333 optelt bij x. 
  • Deze uitkomst is weer het kwadraat van een getal: Noteer dit als q^2.
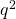  • Dan is 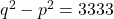q^2-p^2=3333 of (q-p)(q+p)=3333. 
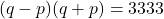  • Nu kan je 3333 schrijven als 1.3333=3.1111=11.303=33.101.
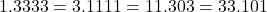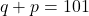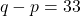  • Zo bekom je bvb het stelsel q+p=101 en q-p=33, waaruit volgt dat p=34 
  • De andere mogelijkheden leveren geen oplossing op voor p tussen 32 en 100.
  • Het gezocht getal is dus 34^2=1156

Nootje 27

Geplaatst op door

 

 

 

Spoiler

  • We zoeken de grootste waarde van een natuurlijk getal x waarvoor \sqrt{x^2-2021} een natuurlijk getal is. Noem dit getal n.
  • Dan geldt: x^2-2021=n^2 of x^2-n^2=2021
  • 2021 heeft 4 delers: 1,43,47 en 2021.
  • Dus is (x-n)(x+n)=1.2021 of (x-n)(x+n)=43.47
  • Uit de eerste gelijkheid volgt dat x-n=1 en x+n=2021. Bijgevolg is x=1011 en n=1010.
  • Uit de tweede gelijkheid volgt dat x-n=43 en x+n=47. Bijgevolg is x=45 en n=2.
  • De grootst mogelijk waarde van x is dus 1011.

Opgave 7

Geplaatst op door

Toon aan dat volgende veeltermfunctie nooit de getalwaarde 33 aanneemt voor willekeurige gehele waarden van x en y.

    \[f(x)=x^5+3x^4y-5x^3y^2-15x^2y^3+4xy^4+12y^5\]

Antwoord

  1. We moeten bewijzen dat de vergelijking

        \[x^5+3x^4y-5x^3y^2-15x^2y^3+4xy^4+12y^5 =33\]

    geen oplossingen heeft voor gehele waarden van x en y. We stellen onmiddellijk vast dat x en y zeker verschillend van nul moeten zijn.

  2. Er bestaan  geen algemene methoden om een vijfde graads vergelijking op te lossen. We zouden  eventueel x^5+3x^4y-5x^3y^2-15x^2y^3+4xy^4+12y^5 -33 kunnen proberen te ontbinden in factoren om zo bovenstaande vergelijking op te lossen. Maar dit lukt niet.
  3. Maar de uitdrukking x^5+3x^4y-5x^3y^2-15x^2y^3+4xy^4+12y^5 kunnen we wel ontbinden als

        \[(x-2y)(x-y)(x+y)(x+2y)(x+3y)\]

  4. Het probleem wordt dus herleid tot : bewijs dat (x-2y)(x-y)(x+y)(x+2y)(x+3y)=33   geen oplossingen heeft voor gehele waarden van x en y.
  5. Nu  heeft 33 als delers \pm1, \pm 3,\pm 11,\pm 33. We kunnen 33 dus hoogstens schrijven als het product van 4 verschillende gehele getallen ( vier positieve ofwel 2 negatieve en 2 positieve). Omdat x en y geheel moeten zijn is het linkerlid van vorige vergelijking steeds het product van 5 verschillende gehele getallen.
  6. Bijgevolg heeft de vorige vergelijking geen oplossingen voor gehele waarden van x en y.