ring | Wiskunde is leuk

Een algebra is eigenlijk een verzameling uitgerust met één of meerdere bewerkingen. We kennen allemaal getallenverzamelingen met daarin een optelling en een vermenigvuldiging. Maar je kan ook een algebra definiëren in een verzameling zonder getallen. Neem bijvoorbeeld de verzameling punten in het vlak (a,b,c,…) en de bewerking $a.b =c$ met c het midden van $[a,b]$ en $a.a=a$ .

Het is een binaire bewerking: met twee punten komt terug een punt overeen.
Deze bewerking is commutatief : 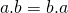$a.b=b.a$ want het midden van $[a,b]$ is hetzelfde als het midden van $[b,a]$ .
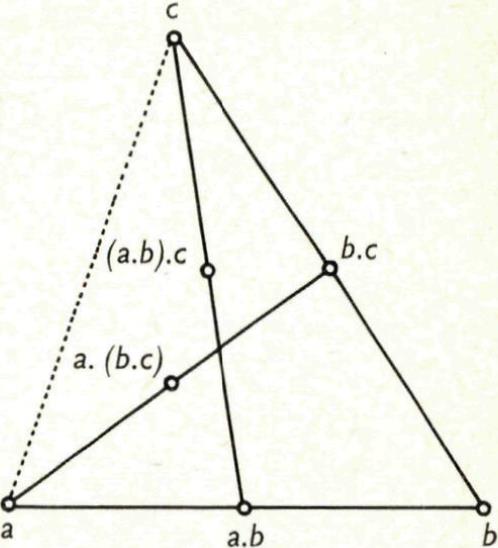
De bewerking is niet associatief: meestal is 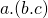$a.(b.c)$ niet gelijk aan 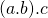$(a.b).c$ . We kunnen de haakjes in uitdrukkingen van de vorm 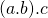$(a.b).c$ dus niet weglaten.
We kunnen ook vergelijking van de vorm 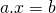$a.x=b$ oplossen. We noteren de oplossing als $\frac{b}{a}$ .
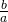We moeten goed oppassen om rekenregels die we kennen uit de getallenleer, niet zomaar over te dragen naar deze nieuwe algebra. Zo is 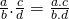$\frac{a}{b}.\frac{c}{d}=\frac{a.c}{b.d}$ maar is 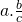$a.\frac{b}{c}$ niet gelijk aan $\frac{a.b}{c}$ .

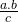Rekenen in dergelijke wiskundige structuur is zeer boeiend en is onderdeel van de abstracte algebra waarin begrippen zoals groepen, ringen, velden, vectorruimten e.d. gebruikt worden om bepaalde ‘algebra’s’met zelfde eigenschappen samen te brengen.

Wiskunde is leuk

Tag archieven: ring

Een nieuwe algebra

Gehelen van Gauss