Topologie is een veralgemening van de meetkunde. Het woord is afgeleid van het Grieks topos(plaats) en logos (studie). Het is een onderdeel van de wiskunde dat zich bezighoudt met eigenschappen in de n-dimensionele ruimte , die bewaard blijven bij continue vervorming (de objecten mogen niet worden gescheurd of geplakt). De term ’topologie’ werd geïntroduceerd in 1847 door de Duitse wiskundige John Benedict Listing ( 1808-1892) in zijn werk Vorstudien zur Topologie . Listing was een leerling van Carl Friedrich Gauss.
In de beginperiode noemde men ‘ deze wiskunde’ : analysis situs, analyse van de positie. Rubbermeetkunde is een betere omschrijving van wat topologie eigenlijk betekent .
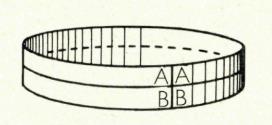
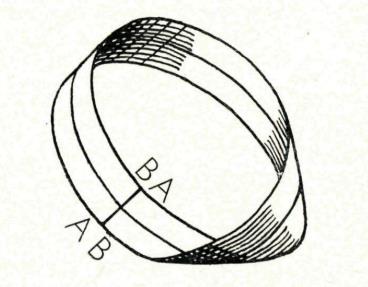
In topologie beschouwt men twee objecten als hetzelfde (homeomorf) als de ene continu vervormd kan worden tot de andere: uitrekken zonder echter te scheuren of verschillende delen samen te plakken.
In de praktijk zijn continue vervormingen echter moeilijk te beschrijven. Er bestaat een andere methode om te zien wanneer twee objecten niet-homeomorf zijn. Hierbij maakt men gebruik van de Euler karakteristiek of de Poincaré-Euler karakteristiek: een geheel getal dat de essentie van de vorm van een topologische ruimte weergeeft.
De Eulerkarakteristiek wordt genoteerd door ![]() . Noteer met h het aantal hoekpunten, met r het aantal ribben en met v het aantal zijvlakken van een figuur.
. Noteer met h het aantal hoekpunten, met r het aantal ribben en met v het aantal zijvlakken van een figuur.
- Voor figuren zoals de cirkel is
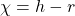 .
. - Voor figuren zoals een bol is
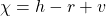 .
.
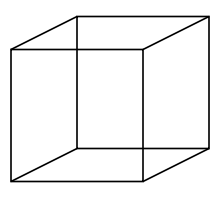
Voor een kubus ( en elk ander Platonisch veelvlak ) is ![]() , want een kubus heeft 8 hoekpunten, 12 ribben en 6 zijvlakken: 8-12+6=2.
, want een kubus heeft 8 hoekpunten, 12 ribben en 6 zijvlakken: 8-12+6=2.
Voor de drievoudige torus kan men aantonen dat ![]() .
.
Het berekenen van de Euler karakteristiek gebeurt via triangulatie, waarop we hier niet verder ingaan. Belangrijk is om te weten dat, als figuren homeomorf zijn, hun Euler karakteristieken dezelfde zijn of door contra positie: als de Euler getallen verschillend zijn , dan zijn de figuren niet homeomorf.