Maandelijks archief: augustus 2018

Ongelijkheid van Jensen

Geplaatst op door

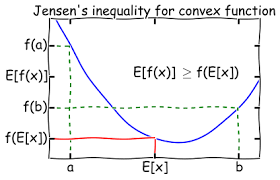
Voor elke functie f waarvan de grafiek ‘hol’ naar onder is , of dus convex (d.w.z dat het verbindingstuk van twee punten van de grafiek altijd boven de grafiek ligt ) geldt volgende ongelijkheid:

    \[f(\dfrac{a_1+a_2+\cdots+\a_n}{n} )\leq \dfrac{f(a_1)+f(a_2)+\cdots+f(a_n)}{n}\]

Deze ongelijkheid staat bekend als de ongelijkheid van Jensen, naar de Deense wiskundige Johan Willem Ludwig Valdemar Jensen (1859-1925).

Uiteraard is er een analoge formule voor concave functies.

Voorbeeld: Als a,b en c positieve hoeken zijn met een som gelijk aan \frac{\pi}{2}, dan is \tan a+ \tan b+\tan c \geq \sqrt{3}.

Tussen 0 en \frac{\pi}{2} is de tangensfunctie convex, dus geldt er volgens Jensen dat \tan (\dfrac{a+b+c}{3}) \leq \frac{1}{3}( \tan a+\tan b+\tan c). Hieruit volgt dat \frac{1}{3}( \tan a+\tan b+\tan c) \geq \tan(\frac{\pi}{6})=\frac{\sqrt{3}}{3}. Vermenigvuldigen met 3 geeft het gevraagde antwoord.

 

Dissectie van een veelhoek

Geplaatst op door

Kan je een veelhoek in stukjes knippen zodat je er een andere veelhoek mee kan bouwen door al de stukjes terug aan elkaar te plakken?  In onderstaand voorbeeld wordt een driehoek getransformeerd in een vierkant.

De stelling van  Wallace–Bolyai–Gerwien zegt dat dit mogelijk is als de twee veelhoeken dezelfde oppervlakte hebben. Het was Farkas Bolyai die het probleem als eerste formuleerde en gerwien bewees de stelling in 1833. Maar Wallace eigenlijk was het Wallace  die ze als eerste bewees in 1807.

Het probleem kan ook gesteld worden in drie dimensie voor veelvlakken en is alzo bekend als derde probleem van Hilbert. Het was Max Dehn die in 1900 bewees dat de stelling niet klopt voor veelvlakken.

Opgave 22

Geplaatst op door

Gegeven: A(x)=x^4+4x^3+8x^2+4x+16. Zoek alle getallen x waarvoor A(x) een volkomen kwadraat is.

Antwoord
  • Het is duidelijk dat A(0)=16 een volkomen kwadraat is. Zijn er nog andere mogelijkheden?
  • A(x) lijkt op B(x)=(x+1)^4=(x^2+2x+1)^2: namelijk A(x)=B(x)+(2x^2+15). Met andere woorden A(x) is zeker groter dan (x^2+2x+1)^2.
  • Neem C(x)=(x^2+2x+2)^2. Wil A(x)=C(x) dan moet 4x-12=0 of x=3.
  • Neem C(x)=(x^2+2x+3)^2. Wil A(x)=C(x) dan moet 2x^2+8x-7=0 . Dit heeft geen gehele oplossingen.
  • Neem C(x)=(x^2+2x+4)^2. Wil A(x)=C(x) dan moet 4x^2+12x=0 . Bijgevolg is  x=0 of x=-3.
  • Neem C(x)=(x^2+2x+5)^2. Wil A(x)=C(x) dan moet 6x^2+16x+9=0 en hier zijn geen gehele oplossingen mogelijk.
  • Neem C(x)=(x^2+2x+6)^2. Dan is A(x)=C(x)-(8x^2+20x+20). Hieruit volgt dat A(x)< C(x) en dus stopt ons onderzoek hier.
  • De enige oplossingen zijn 0,3,-3. Hierbij is A(0)=16=4^2, A(3)=289=17^2 en A(-3)=49=7^2.
  • Gelukkig kunnen we A(x) naar boven begrenzen, anders zou het proces oneindig lang verdergaan.