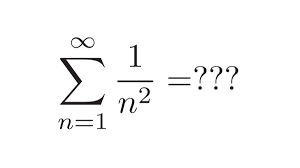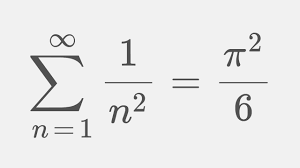In 1873 bewijst Charles Hermite dat het getal e, de basis van de natuurlijke logaritmen, transcendent is. Ferdinand Lindemann toont in 1882 de transcendentie van ![]() aan. Het werk van Lindemann is in feite een handige veralgemening van het resultaat van Hermite. Lindemann bewijst: als z een algebraïsch getal is, verschillend van nul, dan is
aan. Het werk van Lindemann is in feite een handige veralgemening van het resultaat van Hermite. Lindemann bewijst: als z een algebraïsch getal is, verschillend van nul, dan is ![]() transcendent. Transcendente getallen kunnen niet met passer en liniaal geconstrueerd worden.
transcendent. Transcendente getallen kunnen niet met passer en liniaal geconstrueerd worden.
De imaginaire eenheid i is een algebraïsch getal, want i is een wortel van de vergelijking ![]() , bijgevolg is
, bijgevolg is ![]() transcendent. We weten dat
transcendent. We weten dat ![]() . Omdat de som van twee algebraïsche getallen algebraïsch is , kunnen
. Omdat de som van twee algebraïsche getallen algebraïsch is , kunnen ![]() en
en ![]() onmogelijk allebei algebraïsch zijn. Maar als bijvoorbeeld
onmogelijk allebei algebraïsch zijn. Maar als bijvoorbeeld ![]() algebraïsch zou zijn dan is
algebraïsch zou zijn dan is ![]() het ook en omgekeerd. Bijgevolg zijn
het ook en omgekeerd. Bijgevolg zijn ![]() en
en ![]() allebei transcendent en is het duidelijk dat een hoek van 1 radiaal niet te tekenen is met passer en lineaal.
allebei transcendent en is het duidelijk dat een hoek van 1 radiaal niet te tekenen is met passer en lineaal.