Categorie archieven: Weetjes

Axioma’s

Geplaatst op door

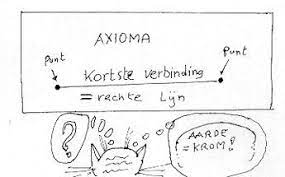
Axioma’s worden op een intuïtieve manier aangebracht als een soort van spelregels. Zonder besef van een deductief systeem heeft bewijsvoering immers geen zin.

We kunnen ook de keuze van een axiomasysteem proberen toe te lichten. We mogen zo een axiomasysteem niet koesteren als een goddelijke waarheid. Anderzijds moeten we ook beseffen dat we geen totale vrijheid hebben in het combineren van axioma’s. Het systeem moet consistent zijn, dus geen tegenspraak bevatten. dat is echter moeilijk na te gaan omdat axioma’s uitspraken zijn over primitieve begrippen. Om de consistentie aan te tonen gaat men gebruik maken van een model: een concrete interpretatie van de ongedefinieerde concepten. We geven een klein voorbeeld:

  • Ax1: Elke x bevat minstens één y.
  • Ax2: Er zijn minstens 2 y’s.
  • Ax3: Als p en q twee y’s zijn, dan is er juist 1 x die zowel p als q bevat.
  • Ax4: Als a een x is, dan is er een y niet in a.

Een mogelijk model is dan : x = rechte en y = punt

Van een axiomasysteem verlangen we nog een andere eigenschap: de onafhankelijkheid. Dit wil zeggen dat geen van de axioma’s kan worden afgeleid uit de andere. Om dat na te gaan moeten we dus modellen construeren die aan alle axioma’s, behalve die ene, voldoen.

 

De wielparadox

Geplaatst op door

Stelt u zich een klein wiel op een groot wiel voor, voorgesteld als twee concentrische cirkels. Voor elk punt op de kleine cirkel is er exact één punt op de grote cirkel en omgekeerd.Je kan dus verwachten dat het samengestelde wiel dezelfde afstand aflegt als het kleine wiel over een staaf rolt of als het grote wiel over de weg rolt. Maar dat kan toch niet, want de omtrek van beide cirkels is verschillend!

Deze paradox werd door Aristoteles beschreven in een oude Griekse tekst Mechanica. 

Cantor heeft veel later aangetoond dat een een-op-eenovereenkomst van punten, niet betekent dat twee krommen even lang moeten zijn. 

De totale verplaatsing van punten op de omtrek van een Aristoteles-wiel kan je zien op onderstaande afbeelding:

Paardenrondgang

Geplaatst op door

Een paardenrondgang is een route bestaande uit paardensprongen op een schaakbord zodat elk veld van het schaakbord juist 1 keer wordt aangedaan.

De oude Arabieren konden dit al: Al-Adli, uit een manuscript uit het jaar 840

Een andere vastgelegde paardenrondgang is een oplossing  uit 1733 van de Franse wiskundige Lemoivre.  Speciaal was de oplossing van Euler . Hij
presenteert een opgevuld schaakbord met een rondgang waarvan de op volgorde genummerde sprongen op het bord ook een (half)magisch vierkant voorstellen met de magische som 260 (de som op de diagonalen klopt niet)

Deze rondgang was niet gesloten, met andere woorden eind en beginpunt vallen niet samen. Dat dit wel kon , liet in 1849 een Hongaar, Wenzelides zien: 

 

Er zijn wel  honderdzes biljoen verschillende gesloten paardronden. In augustus 2003 werd bekend dat de Fransman Meyrignac een 156 jaar oud wiskundig probleem had opgelost; dat van de ‘volledig magische paardronde’. Een door hem afgerichte supercomputer kwam er na 61 dagen rekenen achter dat die paardronde niet bestaat.

 

Het getal van Champernowne

Geplaatst op door

Een 0, gevolgd door een komma en alle natuurlijke getallen op rij, noemt men het getal van Champernowne (Engels wiskundige 1912-2000).

  • Het is een irrationaal getal, want het kan niet geschreven worden als een quotiënt van twee gehele getallen.
  • Sommige irrationale getallen zijn transcendent ( zoals \pi en e): ze zijn geen oplossing van een veeltermvergelijking met gehele coëfficiënten. Het getal van Champernowne is transcendent.
  • Sommige transcendente getallen zijn normaal. Elke eindige reeks van cijfers komt bij benadering even vaak voor als alle andere cijferreeksen van dezelfde lengte. David Champernowne heeft laten zien dat zijn getal normaal is  door aan te tonen dat niet alleen de cijfers 0 tot en met 9 even vaak voorkomen, maar ook alle combinaties van twee cijfers en alle combinaties van drie cijfers.

Het getal van Champernowne is een van de eerste geconstrueerde normale getallen. Hij bedacht het in 1933 en in 1937 bewees de Duitse wiskundige Kurt Mahler dat het transcendent was.