Als in een driehoek twee hoogtelijnen even lang zijn, dan is die driehoek gelijkbenig. Dit is zeer eenvoudig te bewijzen via congruente driehoeken.
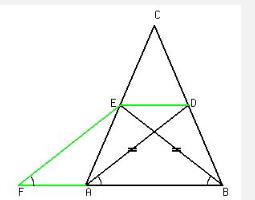
Een driehoek is ook gelijkbenig als er twee even lange zwaartelijnen zijn. Dit bewijs is al iets moeilijker: Stel ![]() , de 2 gelijke zwaartelijnen.
, de 2 gelijke zwaartelijnen.
ED is een middenparallel en dus evenwijdig met AB. Construeer F zodat FADE een parallellogram is. Dan is FEB gelijkbenig en is ![]() . Bijgevolg zijn driehoek DAB en driehoek EAB congruent en zijn de hoeken in driehoek ABC gelijk. Dus is driehoek ABC gelijkbenig.
. Bijgevolg zijn driehoek DAB en driehoek EAB congruent en zijn de hoeken in driehoek ABC gelijk. Dus is driehoek ABC gelijkbenig.
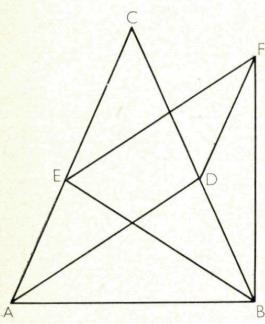
De zaak wordt nog wat complexer als we werken met twee bissectrices. Het bewijs danken we aan de, Zwitserse wiskundige Jacob Steiner ( 1796-1863) en gaat als volgt:
- Neem AD en BE de gelijke bissectrices.
- Construeer F zodat ADFE een parallellogram is. Dan is
 .
. - Veronderstel dat
 .
. - Dan is
 en dus ook
en dus ook  .
. - Omdat driehoek EFB gelijkbenig is, zal
 .
. - Tegenover een grotere hoek staat een grotere zijde in een driehoek, dus
 of
of 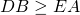 .
. - Als nu 2 driehoeken 2 paar zijden gelijk hebben en de derde zijde is verschillend, zal tegenover een grotere zijde een groter hoek staan. Bijgevolg is
 .
. - Of na verdubbeling
 . Maar dan is
. Maar dan is 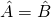 .
. - Dezelfde redenering kunnen we voeren als we starten met de voorwaarde
 .
. - Bijgevolg is driehoek ABC gelijkbenig.