Wiskunde is leuk

Opgave 34: Een integraal…

Geplaatst op 4 maart 2022 door admin

Bereken $A=\int_0^{\frac{\pi}{4}} ln(1+tan x) dx$

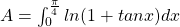
Gewone methoden werken hier niet.
Als een functie f gedefinieerd is op $\left[a,b\right]$ dan kan je de functie spiegelen rond de middelloodlijn van dit lijnstuk en bekom je de functie $g(x)=f(a+b-x)$ .
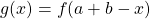Uit de definitie van de bepaalde integraal volgt dan dat $\int_a^bf(x) dx=\int_a^b g(x) dx$ .
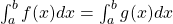Passen we dit toe op de opgave , dan krijgen we: $A=\int _0^{\frac{\pi}{4}} ln(1+tan(\frac{\pi}{4}-x)) dx$ .
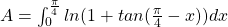Nu is $tan(\frac{\pi}{4}-x)=\frac{1-tan x}{1+tan x}$ .
Zodat $A=\int _0^{\frac{\pi}{4}} ln\Big( \frac{2}{1+ tan x}\Big) dx$ .
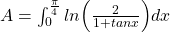Gebruikmakend van de rekenregels voor logaritmen, volgt hieruit dat $A=\int _0^{\frac{\pi}{4}} ln(2) dx -A$ .
Bijgevolg is $A=\frac{\pi}{8} ln(2)$ .