Nootje 18

Geplaatst op 5 januari 2021 door admin

Bereken de oppervlakte van een rechthoekige driehoek in functie van de bissectrice en zwaartelijn betrokken uit de rechte hoek.

Antwoord

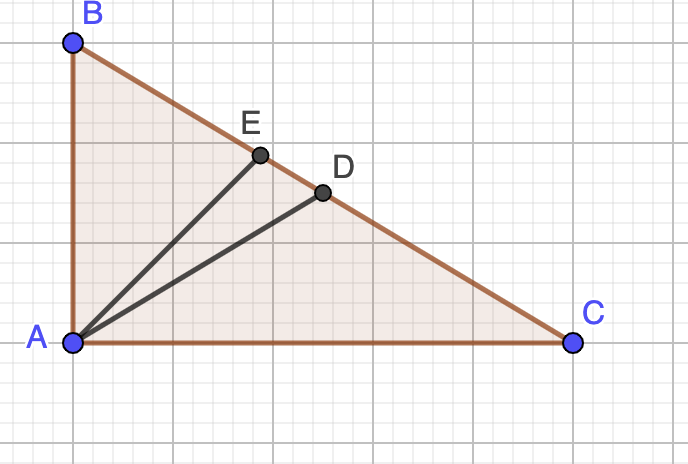
Noem de oppervlakte A en de rechthoekszijden van de rechthoekige driehoek a en b. Noteer met x de lengte van de bissectrice uit A en met y de lengte van de zwaartelijn uit A.
Dan is A de som van de oppervlaktes van ABE en AEC, dus $A=\frac{1}{2}ax \sin 45^\circ+\frac{1}{2}bx \sin 45^\circ$ .
Hieruit volgt dat $A=\frac{\sqrt{2}}{4}(a+b)x$ .
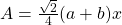Kwadrateren geeft : $A^2=\frac{2}{16}(a^2+b^2+2ab)$ .
Volgens Pythagoras is $a^2+b^2= c^2$ , met c de schuine zijde. Maar de zwaartelijn getrokken naar de schuine zijde is gelijk aan de helft van die schuine zijde. Dus $c=2y$ .
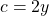Verder is 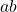$ab$ gelijk aan het dubbele van de oppervlakte van de driehoek, dus $ab=2A$ .
Ingevuld : $A^2=\frac{1}{8}(4y^2+4A)$ .
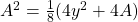Vereenvoudigd: $A^2=\frac{1}{2}x^2y^2+\frac{1}{2}x^2A$ .
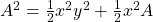Hieruit kan je A oplossen:
$A=\frac{x^2+x\sqrt{x^2+8y^2}}{4}$

Isogonaal toegevoegde punten

Geplaatst op 3 juli 2020 door admin

Om het isogonaal toegevoegd punt van P te berekenen, construeert men het snijpunt van de spiegelbeelden van AP, BP en CP ten opzichte van de respectievelijke bissectrices van de hoeken A,B en C. Het is duidelijk dat de hoeken CAP en QAB gelijk zijn. analoog zijn ook ABP en QBC gelijk en BCP en QCA.

Een andere mogelijke constructie werkt met de voetpuntsdriehoek:

Men tekent de loodlijnen vanuit P op de drie zijden van de driehoek. Hun voetpunten vormen de voetpuntsdriehoek. Construeer nu snijpunt Q van de loodlijnen uit A,B en C op de zijden van de voetpuntsdriehoek. Dan zijn P en Q isogonaal toegevoegd.

Een paar voorbeelden:

Het middelpunt van de ingeschreven cirkel is isogonaal toegevoegd aan zichzelf.
Het hoogtepunt van een driehoek en het middelpunt van zijn omgeschreven cirkel zijn isogonaal toegevoegd.

Lengte zwaartelijn en bissectrice

Geplaatst op 8 oktober 2018 door admin

Om de lengte van een zwaartelijn te berekenen, gebruiken we de cosinusregel in de driehoeken ABD en ACD voor $b^2$ en $c^2$ . Optellen van de formules geeft:

$4z_a^2=2b^2+2c^2-a^2$

Als $a\geq b\geq c$ dan is $z_a \leq z_b\leq z_c$ . Want $4(z_a^2-z_b^2)=3(b^2-a^2)$ . Dus bij de langste zijde hoort de kortste zwaartelijn.

Het berekenen van de lengte van een bissectrice is heel wat lastiger. Noteer $c=|BD|$ en $y=|DC|$ .

Een bissectrice in een driehoek verdeelt de overstaande zijde in de verhouding van de aanliggende zijdes, dus $x:y=c:b$ . Volgens de eigenschappen van evenredigheden volgt hieruit dat $(x+y):y=(c+b):b$ of $y=\frac{ab}{b+c}$ en analoog $x=\frac{ac}{b+c}$ . Teken nu een punt E zodat de hoek ACE gelijk is aan de hoek ADB. Uit de gelijkvormigheid van de driehoeken ACE en ADB volgt dat $|AE|.d_a=bc$ en uit de gelijkvormigheid van de driehoeken DEC en ABD volgt dat $|DE|.d_a=xy$ . Door die twee formules van elkaar af te trekken vinden we dat:

$d_a^2=bc-\frac{a^2bc}{(b+c)^2}$

Net zoals bij de zwaartelijnen kunnen we besluiten dat bij de langste zijde de kortste bissectrice hoort.

Door gebruik te maken van deze formules kan je door algebraïsche berekeningen meetkundige eigenschappen bewijzen, zoals bijvoorbeeld: De langste bissectrice is minstens even lang als de kortste zwaartelijn. Als $a\geq b\geq c$ dan komt dit neer op $d_c \geq z_a$ .

Constructies in verband met ontoegankelijkheid

Geplaatst op 14 februari 2018 door admin

We bestuderen constructies die we normaal gesproken wel kunnen uitvoeren, maar die nu niet uit te voeren zijn omdat bepaalde delen van de figuur ontoegankelijk zijn. Om zulke constructies uit te voeren zijn spiegelingen rond een as uitermate geschikt. We weten immers dat een spiegeling evenwijdigheid, loodrechtheid en ook afstanden en hoeken bewaart. Hierdoor wordt het mogelijk bepaalde gegevens toch bereikbaar te maken.

Bepaal de bissectrice van de twee gegeven rechten.}

Teken een willekeurige rechte $m$ die de twee gegeven rechten (die we $a$ en $b$ noemen) snijdt.
Spiegel de gegeven rechten rond $m$ : $a'$ en $b'$ .
Bepaal het snijpunt $S$ van $a'$ en $b'$ .
Construeer de bissectrice $d$ van $a'$ en $b'$ . Dit is een basisconstructie.
Bepaal tenslotte het spiegelbeeld $d'$ , bij spiegeling van $d$ rond $m$ .

Wiskunde is leuk

Tag archieven: bissectrice