bissectrices | Wiskunde is leuk

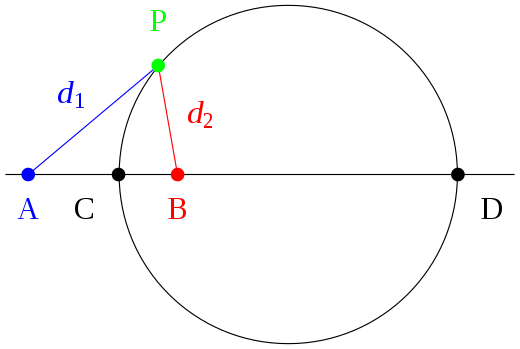
Een cirkel van Apollonius is de meetkundige plaats in het vlak van alle punten p, die bij gegeven punten A en B, voldoen aan

$d(P,A)=r . d(P,B)$

De naam van deze cirkel komt van de Griekse astronoom en wiskundige Apollonius van Perga( 262-190 BC). Hij was degene die kegelsnedes, zoals ellipsen, parabolen en hyperbolen, de namen gaf die we tot op de dag van vandaag nog gebruiken. Zijn achtdelige ”Konika” over kegelsnedes wordt gezien als één van de grootste werken uit de antieke meetkunde. Verder heeft hij enorm bijgedragen aan de astronomie. Dit blijkt uit de, naar hem vernoemde, Apolloniuskrater op de maan.

Merk eerst en vooral op dat als r = 1, dat de meetkundige plaats een rechte is, namelijk de middelloodlijn van $\left[A,B\right]$ .

Veronderstel nu dan dat $r \neq 1$ . Als we de oorsprong in A leggen, de X-as door A en B en B(d,0) noemen, dan is de nodige en voldoende voorwaarde voor (x,y) om op de meetkundige plaats te leggen gegeven door $x^2+y^2=k^2( (x-d)^2+y^2$ . Na wat rekenwerk is dit te herleiden tot

$\big(x-\dfrac{k^2d}{k^2-1}\big)^2+y^2=\dfrac{k^2d^2}{(k^2-1)^2}$

Dit is inderdaad een cirkel met middelpunt $M(\dfrac{k^2d}{k^2-1},0)$ en straal $\dfrac{kd}{k^2-1}$ .

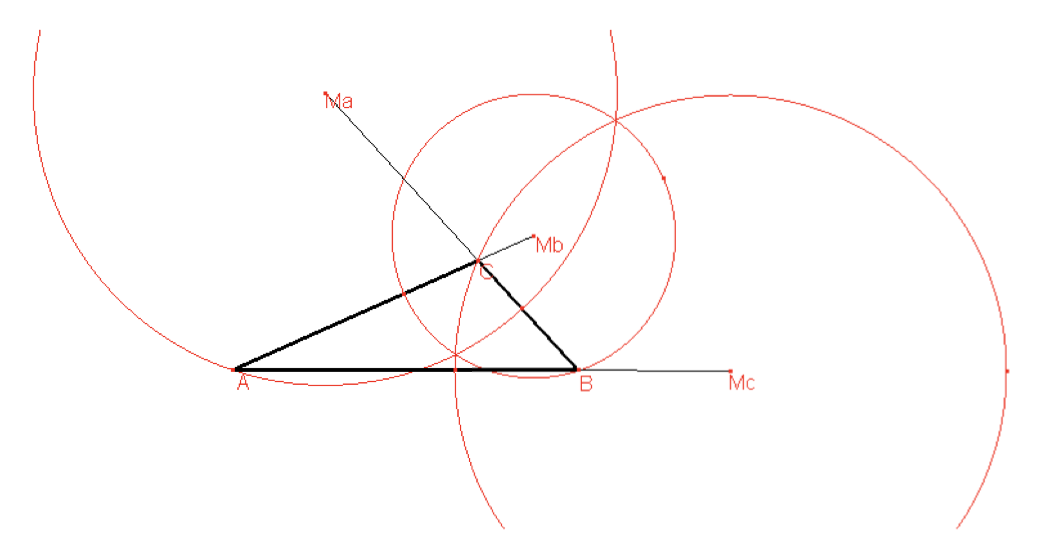
Als C en D de snijpunten zijn van de cirkel met de X-as, dan geldt voor elk punt P van de cirkel dat PC en PD de deellijnen zijn van de driehoek ABP. In een driehoek worden, vanwege deze eigenschap, de cirkels door een hoekpunt en door de snijpunten van de bissectrices door dat hoekpunt met de overstaande zijde de cirkels van Apollonius van die driehoek genoemd.

Een paar opmerkingen:

De Apollonius cirkel door A heeft als verhouding $\frac{c}{b}$ .
Elk van deze cirkels staat loodrecht op de omgeschreven cirkel van de driehoek.
De middelpunten van de drie cirkels liggen op één lijn.

Als in een driehoek twee hoogtelijnen even lang zijn, dan is die driehoek gelijkbenig. Dit is zeer eenvoudig te bewijzen via congruente driehoeken.

Een driehoek is ook gelijkbenig als er twee even lange zwaartelijnen zijn. Dit bewijs is al iets moeilijker: Stel $AD=BE$ , de 2 gelijke zwaartelijnen.

ED is een middenparallel en dus evenwijdig met AB. Construeer F zodat FADE een parallellogram is. Dan is FEB gelijkbenig en is $\widehat{EFA}=\widehat{EBA}=\widehat{DAB}$ . Bijgevolg zijn driehoek DAB en driehoek EAB congruent en zijn de hoeken in driehoek ABC gelijk. Dus is driehoek ABC gelijkbenig.

De zaak wordt nog wat complexer als we werken met twee bissectrices. Het bewijs danken we aan de, Zwitserse wiskundige Jacob Steiner ( 1796-1863) en gaat als volgt:

Neem AD en BE de gelijke bissectrices.
Construeer F zodat ADFE een parallellogram is. Dan is $EF=AD=BE$ .
Veronderstel dat $\hat{A} \leq \hat{B}$ .
Dan is $\widehat{DAE} \leq \widehat{EBD}$ en dus ook $\widehat{DFE} \leq \widehat{EBD}$ .
Omdat driehoek EFB gelijkbenig is, zal $\widehat{DFB} \geq \widehat{DBF}$ .
Tegenover een grotere hoek staat een grotere zijde in een driehoek, dus $DB \geq DF$ of $DB \geq EA$ .
Als nu 2 driehoeken 2 paar zijden gelijk hebben en de derde zijde is verschillend, zal tegenover een grotere zijde een groter hoek staan. Bijgevolg is $\widehat{DAB} \geq \widehat{EBA}$ .
Of na verdubbeling $\hat{A} \geq \hat{B}$ . Maar dan is $\hat{A} = \hat{B}$ .
Dezelfde redenering kunnen we voeren als we starten met de voorwaarde $\hat{A} \geq \hat{B}$ .
Bijgevolg is driehoek ABC gelijkbenig.

Wiskunde is leuk

Tag archieven: bissectrices

De cirkel van Apollonius

Een driehoek is gelijkbenig als…