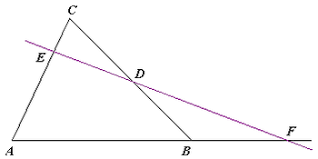
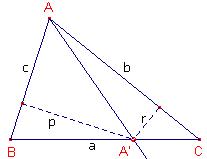
Neem een driehoek ABC. Een rechte l door een hoekpunt A van de driehoek heet hoektransversaal of ceviaan van A. We onderzoeken onder welke voorwaarden de hoektransversalen van A,B en C door één punt gaan.
- Voor een willekeurig punt P op een hoektransversaal beschouwen we de verhouding van de afstanden tot de twee zijden.
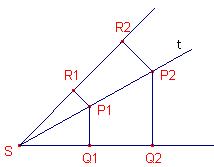 Omdat
Omdat  , is deze verhouding constant. Noem deze constante
, is deze verhouding constant. Noem deze constante  Bij elke transversaal hoort een dergelijke constante. Bereken ze met de klok mee. Nu geldt: De 3 hoektransversalen zijn concurrent als en slechts als
Bij elke transversaal hoort een dergelijke constante. Bereken ze met de klok mee. Nu geldt: De 3 hoektransversalen zijn concurrent als en slechts als 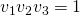 . Zo geldt bijvoorbeeld voor de binnenbissectrices van een driehoek dat
. Zo geldt bijvoorbeeld voor de binnenbissectrices van een driehoek dat  , dus: de drie binnenbissectrices van een driehoek gaan door één punt.
, dus: de drie binnenbissectrices van een driehoek gaan door één punt. - Laat men ook transversalen toe buiten de driehoek, dan moet men aan de constanten
 enkel een ander teken geven. Hetr esultaat van hierboven blijft behouden.
enkel een ander teken geven. Hetr esultaat van hierboven blijft behouden. - We kunnen een hoektransversaal ook kenmerken door de verhouding
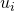 van de oppervlaktedelen waarin de driehoek door de ceviaan verdeeld wordt.
van de oppervlaktedelen waarin de driehoek door de ceviaan verdeeld wordt.
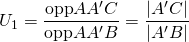 . Het is eenvoudig te zien dat
. Het is eenvoudig te zien dat 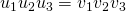 en dus geldt: De 3 hoektransversalen zijn concurrent als en slechts als
en dus geldt: De 3 hoektransversalen zijn concurrent als en slechts als  . Onder deze vorm is de stelling ook gekend als de stelling van Ceva.
. Onder deze vorm is de stelling ook gekend als de stelling van Ceva. - Nu geldt bijvoorbeeld voor de zwaartelijnen van een driehoek dat
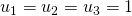 , dus: de drie zwaartelijnen van een driehoek gaan door één punt.
, dus: de drie zwaartelijnen van een driehoek gaan door één punt. - We kunnen dit ook ondzerzoeken voor de drie hooigtelijnen.
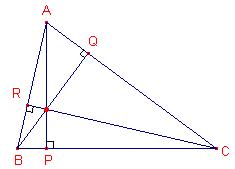
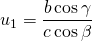 ,
,  en
en 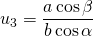 en dus is
en dus is  . Bijgevolg geldt: de drie hoogtelijnen van een driehoek gaan door één punt.
. Bijgevolg geldt: de drie hoogtelijnen van een driehoek gaan door één punt.