Tag archieven: fractalen

De kromme van Peano

Geplaatst op door
 
De Peano-kromme, genoemd naar de Italiaanse wiskundige Giuseppe Peano (1858-1932), is een van de meest intrigerende concepten in de wiskunde. Deze curve, die in 1890 werd geïntroduceerd, was een revolutionaire ontdekking omdat het aantoonde dat een continue lijn een volledig tweedimensionaal vlak kan vullen.
 
De constructie van de Peano-kromme is gebaseerd op een iteratief proces. Het begint met een eenvoudige lijn die in een vierkant wordt getekend. Deze lijn wordt vervolgens herhaaldelijk opgesplitst en gevouwen volgens een specifiek patroon. Na oneindig veel stappen vult de curve het hele vierkant, waarbij elk punt in het vierkant wordt bereikt door de lijn. 
 
 
  • Basisstap: Begin met een vierkant en een eenvoudige lijn die het vierkant in een patroon doorkruist (bijvoorbeeld een zigzaglijn).
  • Iteratiestap: Verdeel het vierkant in een 3×3 raster (dus 9 kleinere vierkanten). Vervang de oorspronkelijke lijn in elk van deze kleinere vierkanten door een verkleinde versie van het oorspronkelijke patroon.
  • Herhaling: Herhaal dit proces oneindig vaak, waarbij het vierkant steeds verder wordt onderverdeeld in kleinere vierkanten, en de lijn steeds complexer wordt.

Voor Peano’s ontdekking werd aangenomen dat een continue functie van een eendimensionale ruimte (zoals een lijn) naar een tweedimensionale ruimte (zoals een vlak) niet het hele vlak kon vullen. Peano bewees het tegendeel en opende daarmee de deur naar nieuwe inzichten in topologie en fractale  meetkunde. Een belangrijke eigenschap van de Peano-kromme is dat deze continu maar niet differentieerbaar is. Dit betekent dat de curve geen scherpe hoeken heeft, maar ook geen vloeiende afgeleide – een kenmerk dat typisch is voor fractale structuren.

De fractale of Hausdorff dimensie van de Peano-kromme is 2.  Neem bijvoorbeeld een andere fractale figuur , zoals de sneeuwvlok van Koch. Dit is geen ruimtevullende kromme; zijn fractale dimensie is ongeveer 1,26.

Een ander voorbeeld van een ruimtevullende kromme is de kromme van Hilbert:

Julia fractaal

Geplaatst op door

Neem de functie f(x)=x^2+c en neem een willekeurige startwaarde x_1. Bereken de functiewaarde van x_0 en noem die x_1. Bereken vervolgens de functiewaarde van x_1 en noem die x_2. We verkrijgen zo een rij getallen

    \[x_{n+1}=f(x_n)\]

Gaston Julia ( 1893-1978) publiceerde in 1919 zijn boek Mémoire sur l’iteration des fonctions rationelles waarin hij het iteratief gedrag van deze functie(s) onderzocht.

We bestuderen nu

de relatie z_{n+1}=f(z_n) in het complexe vlak. Als de rij z_0,z_1,z_2,... begrensd is, dan gaan we de startwaarde z_0 plotten. De verzameling punten in het complexe vlak waarvoor de rij begrensd is noemen we de Julia verzameling horend bij c.

Er zijn op basis hiervan twee verzamelingen te construeren: de verzameling van de punten z0 waarvoor het iteratieve proces begrensd is (de Julia-set bij C) en  de verzameling van de punten z0 waarvoor de verzameling niet-begrensd is. De rand van het “begrensdheidsgebied” wordt een “fractaal” genoemd, de Julia-fractaal bij c.

Dit levert zeer mooie figuren :

Of de san Marco fractaal en het dendriet…

 

Dimensie

Geplaatst op door

Rechthoeken, driehoeken, cirkels,… zijn lange tijd de meest bestudeerde meetkundige figuren geweest. In realiteit komen deze figuren echter zelden voor. Als we eens een luchtfoto bekijken van de kustlijn van een willekeurig continent, dan blijkt die lijn niet meer zo ‘glad’ te zijn dan bij een rechthoek. Er is hier spraken van een fractaal.

De naam fractaal werd ingevoerd door Benoit Mandelbrot, die heeft willen aantonen dat de ons omgevende natuur rijk is aan fractals.

We willen het hier vooral hebben over de dimensie van dergelijke objecten. Dit artikel is geschreven door Luca Pignatti, leerling van 6WEWIe2 aan het H.Drievuldigheidscollege in Leuven.

We zoeken een  alternatieve definitie  voor de dimensie van een object. Daarvoor voeren we  een onderzoek naar dimensies op objecten waarvan we de dimensie reeds kennen. Een 1-dimensioneel lijnstuk, een 2-dimensioneel oppervlak en een 3-dimensionele kubus. Wanneer je elk voorwerp met een factor vergroot of verkleint bekom je hetzelfde voorwerp maar met een verschillende afmeting. Deze afmeting zou je ook kunnen beschouwen als de massa van het voorwerp, ook al is dit niet helemaal juist, een lijnstuk heeft geen massa. Het is wel een goede manier om het te visualiseren. Probeer je voor te stellen dat de voorwerpen uit metaal gemaakt zijn, metalen draad, metaalplaat en massief metaal. Een voorbeeld: verkleinen met factor ½

dimensie 1, lengte ½ , massa ½

dimensie 2, lengte ½, massa 1/4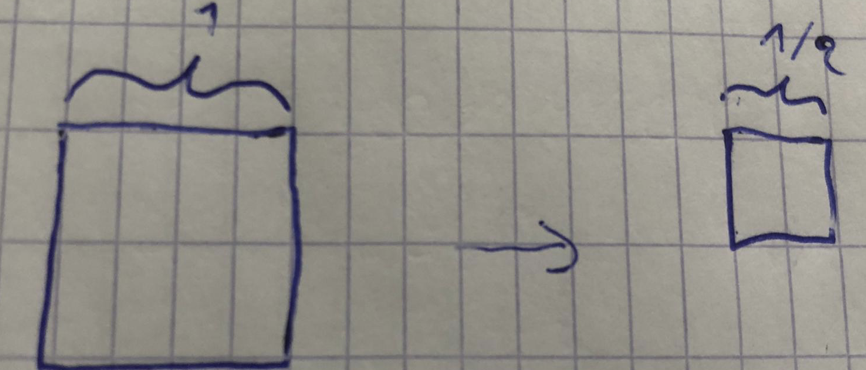

dimensie 3, lengte ½, massa 1/8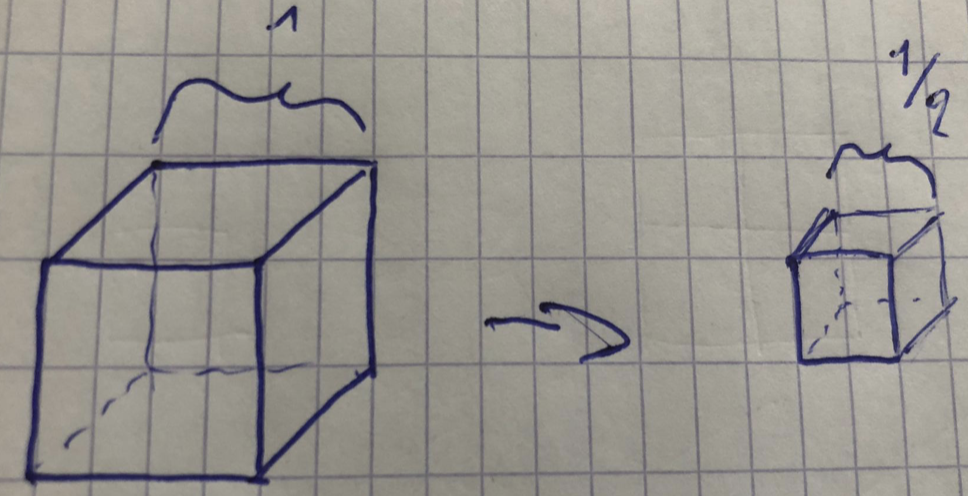 

We vinden dat wanneer de lengte gehalveerd wordt,  de massa van het voorwerp met diezelfde factor tot de macht van de dimensie verheven wordt. Dit geldt niet enkel voor factor ½ maar voor elk ander reëel, positief getal. zo krijgen we de formule

    \[s^d=m\]

Hierbij is s de vergrotingsfactor, m de massa na de transformatie en  d  de dimensie .

Dit verband kan ons helpen met zoeken naar de dimensies van bepaalde fractalen, zoals de driehoek van Sierpinski. De driehoek van Sierpiński is een fractaal die werd ontdekt door de Poolse wiskundige Wacław Sierpiński. Uit een gelijkzijdige driehoek wordt de driehoek verwijderd die gevormd wordt door de middens van de drie zijden. Vervolgens wordt deze procedure herhaald in elk van de drie overgebleven driehoeken.

We zien dat wanneer we de zijde van de driehoek met factor ½ verkleinen dat de massa (oppervlakte)  van het voorwerp er na tot \frac{1}{3} van de massa ervoor is. Wanneer we onze formule invullen voor s=1/2 en m=1/3 vinden we (1/2)D = (1/3). De dimensie zou dan gelijk moeten zijn aan \log_23\approx 1,58496.

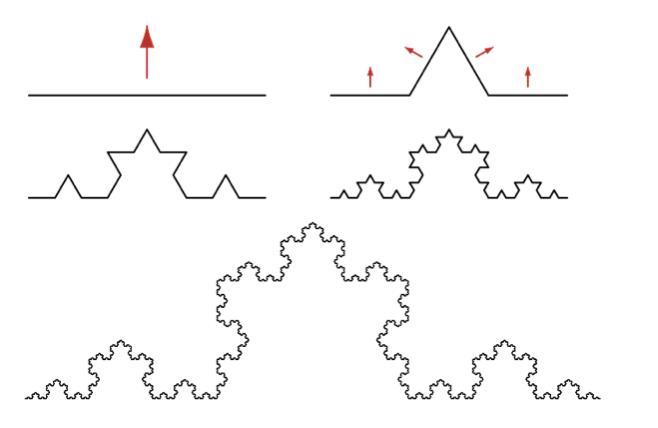
Laten we even kijken naar de kromme van Koch:

We vinden s=1/3, m=1/4 en dus is de dimensie van de Kochkromme gelijk aan \log_34\approx 1,26186.

De dimensie van onze fractals is dus niet langer een natuurlijk getal, maar wel een breuk! Iets tussen dimensie 1 en dimensie 2.