Tag archieven: meetkunde

Middendriehoek

Geplaatst op door

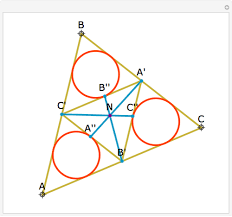
De middendriehoek van een driehoek ABC is de driehoek SRQ, gevormd door de middenparallellen van de gegeven driehoek. 

Enkele eigenschappen:

  • De oppervlakte van de middendriehoek is \frac{1}{4} van de oppervlakte van de gegeven driehoek.
  • De omtrek van de middendriehoek is 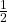\frac{1}{2} van de omtrek van de gegeven driehoek.
  • De middendriehoek  is gelijkvormig met de gegeven driehoek: de middendriehoek is het beeld van ABC onder een homothetie met centrum het zwaartepunt van ABC en als factor -\frac{1}{2}.
  • De middendriehoek en driehoek ABC hebben hetzelfde zwaartepunt.
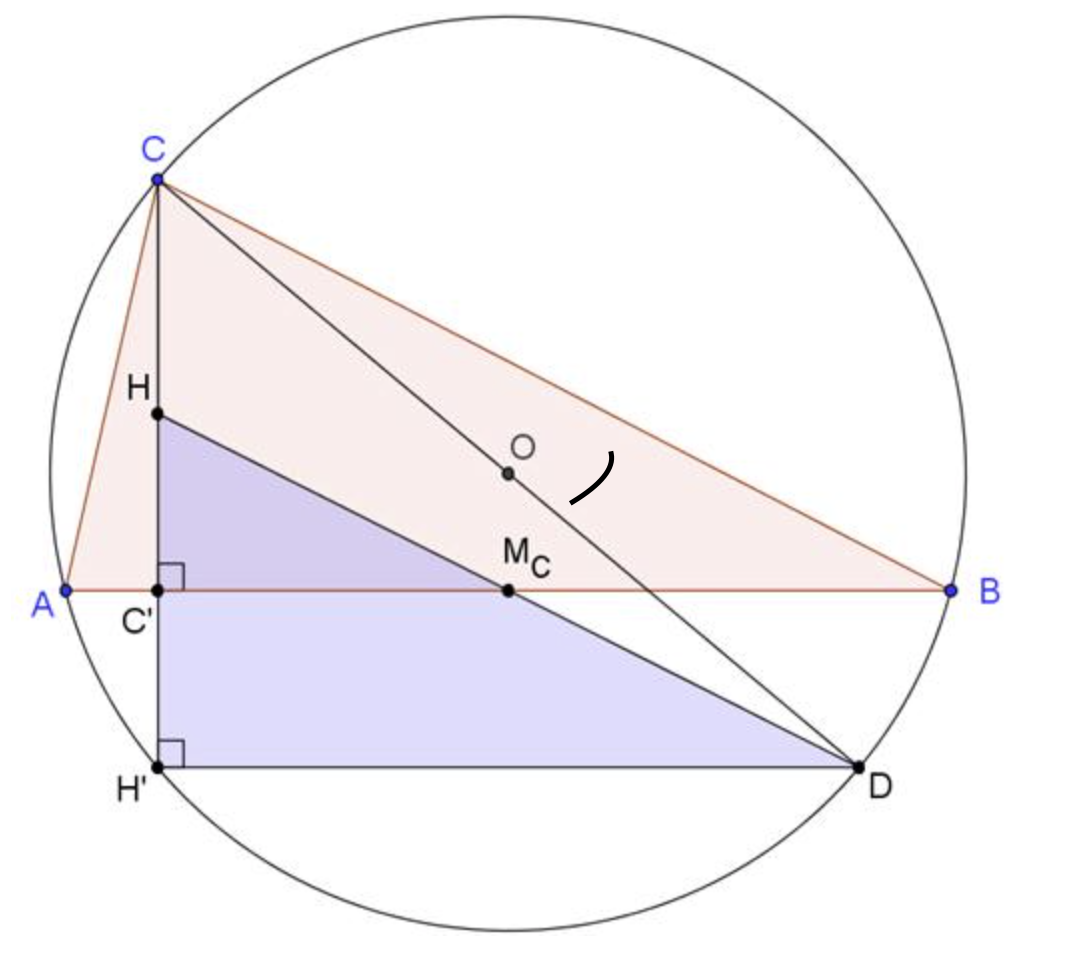
  • Het hoogtepunt van de middendriehoek valt samen met het middelpunt van de omgeschreven cirkel van driehoek ABC.
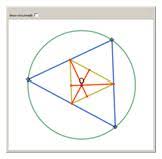
  • De voetpunten van de hoogtelijnen van driehoek ABC liggen op de omgeschreven cirkel van de middendriehoek.

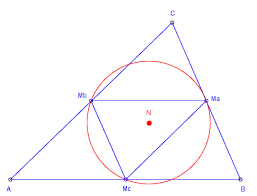
  • De omgeschreven cirkel van de middendriehoek is de negenpuntscirkel van ABC ( de cirkel door de middens van de zijden, de voetpunten van de hoogtelijnen en de middens van de lijnsegmenten van uit de hoekpunten naar het hoogtepunt ).
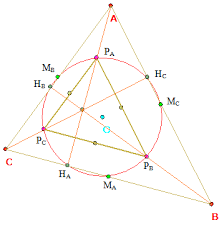
  • En dan nog deze afsluiter: bedenk zelf maar de stelling!

Een meetkundige parel

Geplaatst op door

Onlangs vond ik volgende stelling die ik helemaal niet kende. Een echt pareltje: De spiegelbeelden van het hoogtepunt van een driehoek ABC rond de zijden en rond de middens van de zijden liggen op de omgeschreven cirkel van ABC.

H’ is het spiegelbeeld van H (hoogtepunt) rond de zijde AB en CD is een middellijn van de omgeschreven cirkel.

  • \widehat{CDB} is een rechte hoek, als omtrekshoek op een halve cirkel. Omdat AH loodrecht op BC staat, zijn BD en AH evenwijdig.
  • Analoog is AD ook evenwijdig met BH.
  • Dus is AHBD een parallellogram. 
  • Omdat de diagonalen van een parallellogram elkaar midden doordelen is M_c het midden van AB en dus is D inderdaad het spiegelbeeld van H bij een puntspiegeling rond het midden van B.
  • Omdat HC’=C’H’ is C'M_c de middenparallel van driehoek HH’D en staat DH’ loodrecht op CC’ omdat DH’ evenwijdig is met C'M_c.
  • Dus is \widehat{CH'D}=90^\circ  en wegens de eigenschappen van omtrekshoeken ligt dus H’ op de omgeschreven cirkel van driehoek ABC.

Stelling van Viviani

Geplaatst op door

Kies een punt binnen een gelijkzijdige driehoek. Bereken de afstand van dit punt tot de drie zijden van de driehoek. Waar je dit punt ook plaatst de som van die afstanden is gelijk aan de hoogte van de driehoek.

De stelling kan eenvoudig bewezen worden. Noem het punt P en de driehoek ABC. De oppervlakte van ABC is gelijk aan de som van de oppervlakten van de driehoeken PAB, PAC en PBC. Hieruit volgt het gestelde.

Deze stelling is vernoemd naar de Italiaanse wiskundige en wetenschapper Vincenzo Viviani( 1622-1703).

We kunnen de eigenschap ook veralgemenen tot een regelmatige n-hoek. In dat geval is de som van de afstanden vanuit een punt binnen de veelhoek naar de n zijden gelijk aan n keer het apothema van de veelhoek.Zelfs het omgekeerde is waar: wanneer de som van de minimale afstanden naar elk van de zijden van een veelhoek onafhankelijk is van het gekozen punt binnen de veelhoek, dan is het een regelmatige veelhoek .

6. Wiskunde in het oude Indie

Geplaatst op door

 

De eerste belangrijke beschaving in het Indus gebied was de Harappa-beschaving rond 2000 voor Christus

Het Vedische volk kwam India rond 1500 voor Christus binnen vanuit wat nu  Iran is.  In deze Vedische beschaving was de bevolking verdeeld in verschillende sociale klassen. de leiding berustte bij de priesterklasse, de Brahmanen. Hun heilige teksten staan bekend staan ​​als de Veda’s. De teksten dateren van ongeveer de 15e tot de 5e eeuw voor Christus en werden gebruikt voor offerrituelen die het belangrijkste kenmerk van de religie waren. De belangrijkste van deze documenten zijn de Baudhayana Sulbasutra geschreven rond 800 voor Christus en de Apastamba Sulbasutra geschreven rond 600 voor Christus. Minder gekend zijn de Manava Sulbasutra geschreven rond 750 voor Christus en de Katyayana Sulbasutra geschreven rond 200 voor Christus.

De Sulbasutra’s zijn bijlagen bij de Veda’s die regels geven voor het bouwen van altaren. Als het rituele offer succesvol zou zijn, moest het altaar zich  zeer precieze afmetingen hebben. Om de goden tevreden te stellen, moest alles met een zeer precieze formule worden uitgevoerd, dus werd wiskundige nauwkeurigheid van het grootste belang geacht. 

Alles wat bekend is van Vedische wiskunde is vervat in de Sulbasutras. Sommige historici beweren dat de wiskunde, meer speciaal de meetkunde, ook moet hebben bestaan ​​als ondersteuning van de astronomie.

Een paar voorbeelden van hun meetkundige kennis:

  • Een vierkant dat de som is van twee andere vierkanten
  • De diagonaal van een vierkant geeft een vierkant van dubbele oppervlakte.
  • Een vierkant dat gelijk is aan een cirkel (komt overeen met een waarde voor pi van ongeveer 3,00444)
  • De som van de oppervlakten van vierkanten van de lengte en breedte van een rechthoek geeft het vierkant van de diagonaal van de rechthoek.
  • Vermeerder de eenheid met een derde en dit derde met zijn vierde en verminder dat met het 34ste deel van dat vierde. zo bekom je een benadering voor de vierkantswortel van 2: 1,414215

De Sulbasutra’s bevatten geen enkel bewijs van de regels die ze beschrijven. Sommige regels, zoals de methode om een ​​vierkant te construeren dat gelijk is aan een bepaalde rechthoek, zijn exact. Anderen, zoals het construeren van een vierkant gelijk aan dat van een bepaalde cirkel, zijn benaderingen. 

 

 

Niet-Euclidische meetkunde

Geplaatst op door

 

De meetkunde, die we dagelijks gebruiken, wordt Euclidische meetkunde genoemd, ter ere van Euclides, die tussen 330 en 320 voor Christus een aantal boeken, genaamd „Elementen” geschreven heeft.

Hierin wordt  de meetkunde opgebouwd met stellingen vertrekkend van een vijftal postulaten of axioma’s: 
1. Door 2 verschillende punten gaat juist 1 rechte.
2. Een lijnstuk kan naar beide kanten onbeperkt worden
    verlengd.
3. Er kan met elk middelpunt en elke straal een cirkel
    getrokken worden.
4. Alle rechte hoeken zijn gelijk.
5. Door een punt P buiten een rechte , gaat precies één rechte
    die evenwijdig loopt met  de eerste rechte.

Dit laatste axioma staat bekend als het parallellenpostulaat.
Eeuwen heeft men gedacht dat men dit postulaat kon bewijzen aan de hand van de andere vier axioma’s. Trouwens de formulering van het parallellenpostulaat was oorspronkelijk anders.  De gegeven formulering komt van John Playfair. Deze formulering stamt uit 1795 en staat bekend als “Playfair’s axioma” . Een andere gelijkwaardige formulering van dit postulaat is dat de hoekensom van een driehoek gelijk is aan 180°.

Het duurde tot de 19 de eeuw voor het juist inzicht er kwam en wel bij 3 wiskundigen ongeveer gelijktijdig en waarschijnlijk onafhankelijk van elkaar: C.F.Gauss, J.Bolyai en I.Lobatschefsky.

Het was Joha,, Bolyai die tot het inzicht kwam dat het mogelijk was een meetkunde op te stellen, waarin door een punt buiten een rechte oneindig veel rechten gaan die de gegeven rechte niet snijden. Hij publiceerde zijn ideeën in 1832 en gaf zo gestalte aan de hyperbolische meetkunde. De som van de hoeken van een driehoek is hier minder dan 180°.  In de hyperbolische meetkunde wordt dus niet meer aan het parallellenpostulaat voldaan. 
Later werd ook de elliptische meetkunde ontdekt. Elliptische meetkunde is een niet-Euclidische meetkunde, waarbij door een punt buiten een rechte  geen andere rechten bestaat die de gegeven rechte niet snijdt.

De gewone meetkunde is dus niet de meetkunde, maar een  meetkunde. Met andere axioma’s krijgen we een ander soort meetkunde.