Een sangaku is van nature uit een Japanse puzzel uit de Euclidische meetkunde. Vanuit een afbeelding wordt er gevraagd een eigenschap of stelling te herkennen of een berekening uit te voeren. Laten we starten met een eenvoudig voorbeeld:
Antwoord
- Er wordt hier gevraagd naar de oppervlakte van het gele vierkant.
- De oppervlakte van het grote vierkant is
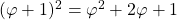 . Nu is
. Nu is 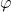 de gulden snede, dus is
de gulden snede, dus is 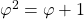 , zodat de oppervlakte van het grote vierkant gelijk is aan
, zodat de oppervlakte van het grote vierkant gelijk is aan  .
. - Nu moet je vier driehoeken met schuine zijde
 aftrekken. De kleinste rechthoekszijde vindt men door gelijkvormige driehoeken te beschouwen en heeft dan als lengte
aftrekken. De kleinste rechthoekszijde vindt men door gelijkvormige driehoeken te beschouwen en heeft dan als lengte 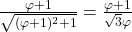 .
. - Zo wordt de oppervlakte van het gele vierkant uiteindelijk
 . Hierbij gebruiken we de eigenschap dat
. Hierbij gebruiken we de eigenschap dat  .
.

