Wiskunde is leuk

Nootje 23

Geplaatst op 15 juli 2021 door admin

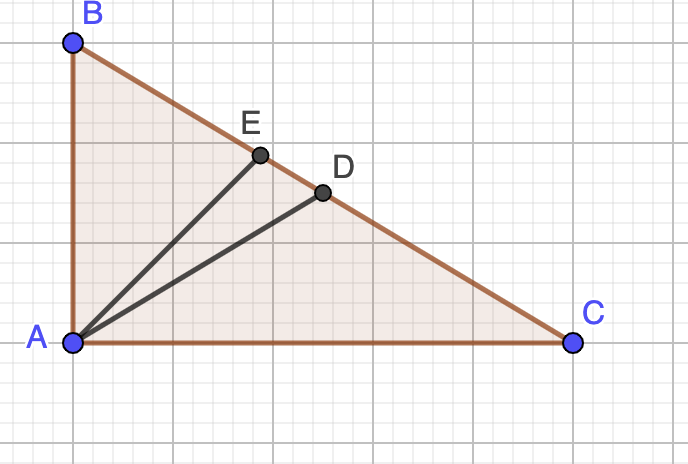
Bereken de oppervlakte van het gebied bepaald door
$|x|+|y|+|x+y|\leq 1$

Antwoord

In het eerste kwadraat is x>0 en y>0 en dus ook x+y>0. De gegeven ongelijkheid wordt dan $x+y\leq \frac{1}{2}$ .
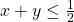In het derde kwadrant is x<0 en y<0 en dus ook x+y<0. De ongelijkheid wordt dan $x+y\geq -\frac{1}{2}$ .
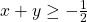In het tweede kwadrant is x<0 en y>0. Als x+y>0 wordt de ongelijkheid $y\leq \frac{1}{2}$ . Is echter x+y<0, dan verkrijgen we $x\geq -\frac{1}{2}$
In het vierde kwadrant tenslotte is x>0 en y<0. Als x+y>0, dan is de ongelijkheid 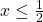$x\leq \frac{1}{2}$ . Is daarentegen x+y<0, dan krijgen we $y\geq - \frac{1}{2}$
Het stelsel van al die ongelijkheden geeft volgend gebied in het vlak:
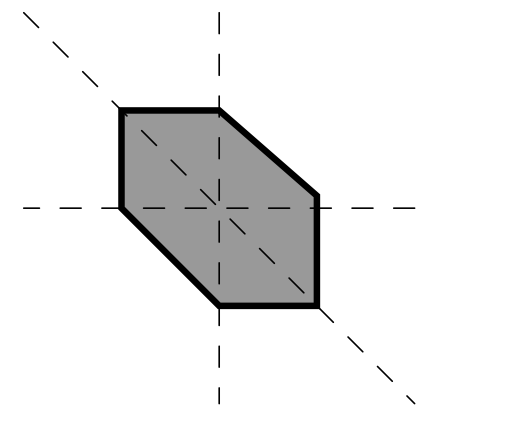
In deze figuur herkennen we gemakkelijk drie vierkanten met zijde 1. De oppervlakte is dus 3 oppervlakte eenheden

Nootje 18

Geplaatst op 5 januari 2021 door admin

Bereken de oppervlakte van een rechthoekige driehoek in functie van de bissectrice en zwaartelijn betrokken uit de rechte hoek.

Antwoord

Noem de oppervlakte A en de rechthoekszijden van de rechthoekige driehoek a en b. Noteer met x de lengte van de bissectrice uit A en met y de lengte van de zwaartelijn uit A.
Dan is A de som van de oppervlaktes van ABE en AEC, dus $A=\frac{1}{2}ax \sin 45^\circ+\frac{1}{2}bx \sin 45^\circ$ .
Hieruit volgt dat $A=\frac{\sqrt{2}}{4}(a+b)x$ .
Kwadrateren geeft : $A^2=\frac{2}{16}(a^2+b^2+2ab)$ .
Volgens Pythagoras is $a^2+b^2= c^2$ , met c de schuine zijde. Maar de zwaartelijn getrokken naar de schuine zijde is gelijk aan de helft van die schuine zijde. Dus $c=2y$ .
Verder is $ab$ gelijk aan het dubbele van de oppervlakte van de driehoek, dus $ab=2A$ .
Ingevuld : $A^2=\frac{1}{8}(4y^2+4A)$ .
Vereenvoudigd: $A^2=\frac{1}{2}x^2y^2+\frac{1}{2}x^2A$ .
Hieruit kan je A oplossen:
$A=\frac{x^2+x\sqrt{x^2+8y^2}}{4}$