Tag archieven: stelling Apollonius

Stelling van Stewart

Geplaatst op door

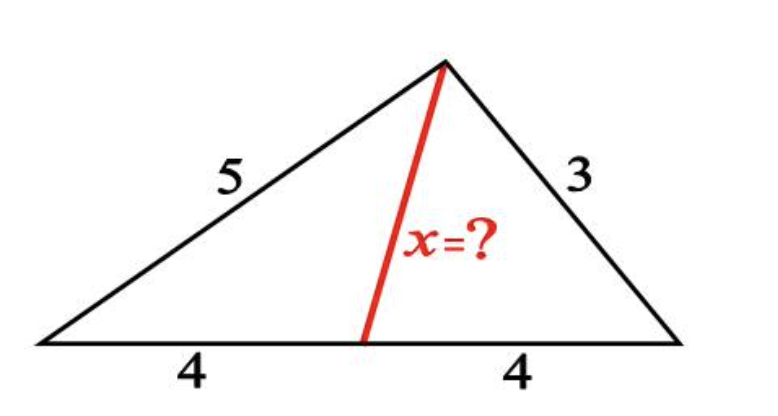
Onlangs vond ik op Facebook volgende opgave:

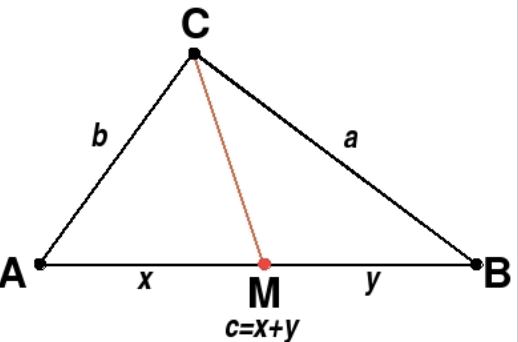
Matthew Stewart (1717-1785), een Schots wiskundige, publiceerde in 1746 een stelling waarmee je dit eenvoudig kan oplossen. De stelling berekent de lengte van een hoektransversaal  d=|CM| in een driehoek:

    \[cd^2=xa^2+yb^2-cxy\]

Het bewijs ervan is eerder eenvoudig: gebruik 2 keer de cosinus regel om resp a^2 en b^2 te berekenen.

Voor die hoektransversaal kan men speciale ‘lijnen’ in de driehoek kiezen:

  • Als d de zwaartelijn is uit C, dan herleidt de formule zich tot

        \[d^2=\frac{1}{2}(a^2+b^2-\frac{1}{2}c^2)\]

    De gegeven opgave van Facebook heeft dan als oplossing x=1.
  • Als d de bissectrice is uit C, dan krijgen we

        \[d^2=ab-xy\]

    Het bewijs steunt op de bissectrice stelling x:y=b:a

 

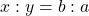
Dit pareltje uit de vlakke meetkunde  wordt ook wel de stelling van Apollonius genoemd. Maar Apollonius van Perga formuleerde de stelling enkel voor x=y, dus het geval dat de hoektransversaal de zwaartelijn is.