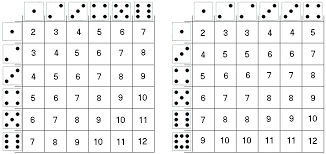
Andere dobbelstenen | Wiskunde is leuk

Iedereen kent deze klassieke dobbelsteen. Nemen we nu twee van dergelijke dobbelstenen en berekenen we de som van het aantal ogen:

De vraag is nu: kunnen we geen ander stel van dobbelstenen vinden die dezelfde verdeling geeft?

We stellen onze gewone dobbelsteen voor door
$x^6+x^5+x^4+x^3+x^2+x$
Je leest deze veelterm als: er is 1 kant met 6stippen, 1 kant met 5 stippen,…
Wanneer je nu met 2 dobbelstenen gooit, voer je eigenlijk het product uit van die veelterm met zichzelf en krijg je dus $(x^6+x^5+x^4+x^3+x^2+x)^2=x^{12}+2x^{11}+3x^{10}+...+x^2$ Je leest in deze uitkomst dan volledig het bovenstaande schema.
Noem nu het gezochte stel andere dobbelstenen door f(x) en g(x).
We willen dat $f(x).g(x)=x^{12}+2x^{11}+3x^{10}+...+x^2$ .
De ontbonden vorm van de veelterm in het rechterlid is
$x^2(x+1)^2(x^2+x+1)^2(x^2-x+1)^2$
Hieruit volgt dat we opzoek moeten naar een a,b,c en d zodat
$f(x)=x^a(x+1)^b(x^2+x+1)^c(x^2-x+1)^d$

$g(x)=x^{2-a}(x+1)^{2-b}(x^2+x+1)^{2-c}(x^2-x+1)^{2-d}$
Omdat we zes zijvlakken hebben moet 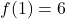$f(1)=6$ , dus moet $2^b3^c=6$ of $b=c=1$
Verder kan a zeker niet nul zijn want dan zou f(0) niet 0 zijn. En dus kan a ook niet 2 zijn. Bijgevolg is a=1.
Voor d=1 krijgen we de klassieke dobbelstenen.
Nemen we d=0, dan is 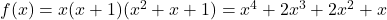$f(x)=x(x+1)(x^2+x+1)=x^4+2x^3+2x^2+x$ . Dis geeft een dobbelsteen met op de zijvlakken 4/3/3/2/2/1
De andere dobbelsteen geeft dat 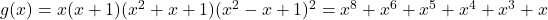$g(x)=x(x+1)(x^2+x+1)(x^2-x+1)^2=x^8+x^6+x^5+x^4+x^3+x$ of een dobbelsteen met op de zijvlakken 8/6/5/4/3/1.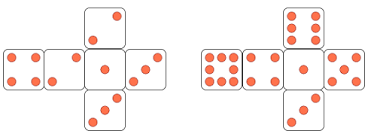
Hier zie je dat de verdeling inderdaad hetzelfde is tussen de 2 sets van dobbelstenen.