Categorie archieven: Opgaven

Opgave 41

Geplaatst op door

Veronderstel dat n een oneven getal en schrijf dan op een blad papier alle  natuurlijke getallen 1,2,3,…., 2n. Dan laat je er twee willekeurige getallen hieruit kiezen  en schrap ze en schrijf erbij het verschil van het grootste men het kleinste van die twee getallen. Toon aan dat, bij herhaling, het laatste overblijvende getal zeker oneven is.

Antwoord

  • Noteer met S de som van alle opgeschreven getallen. Dan is S=1+2+…+2n of

        \[S=n(2n+1)\]

  • Dus S is oneven omdat n oneven is en 2n+1 ook.
  • Neem nu twee willekeurig neergeschreven getallen a en b  en stel a>b , dan wordt de nieuwe som S'=S-a-b+a-b=S-2b. Omdat je een even getal aftrekt van een oneven S, zal de nieuwe som S’ ook oneven zijn. Voor het geval dat a<b is dit analoog.
  • De pariteit van de som van alle nog beschikbare getallen is dus een invariante. Met andere woorden, telkenmale we twee getallen schrappen en vervangen door het verschil blijft de som oneven.
  • Dus het laatst overgebleven getal is oneven.

Opgave 40

Geplaatst op door

Een convexe zeshoek is ingeschreven in een cirkel met straal r. Twee zijden van deze zeshoek hebben als lengte 7 eenheden , terwijl de vier overige als lengte 20 eenheden hebben. Bepaal de straal van de cirkel.

Antwoord

  • Wat de volgorde van de zijden is, steeds moet minstens aan één zijde met lengte 7 een zijde met lengte 20 aanliggend zijn. Noem de middelpuntshoek tegenover de zijde met lengte 20  eenheden 2a en de middelpuntshoek tegenover de zijde met lengte 7 eenheden 2b.
  • Door het apothema te trekken op de zijden van de zeshoek vinden we dat 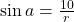\sin a=\frac{10}{r} en \sin b=\frac{3,5}{3}.
  • De som van alle middelpuntshoeken is 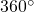360^\circ, dus 2*2b+4*2a=360^\circ. Hieruit volgt dat b+2a=90^\circ.
  • Dan geldt er dat \sin b=\cos 2a=1-2\sin^2 a
  • Volgens een vorig punt is dus 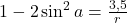1-2\sin^2 a=\frac{3,5}{r}. Of

        \[1-2\Big(\frac{10}{r}\Big)^2=\frac{3,5}{r}\]

  • Dit geeft een vierkantsvergelijking: 2r^2-7r-400=0
  • De enige positieve oplossing van deze vergelijking is 16.
  • De straal is 16 eenheden lang.

Opgave 39

Geplaatst op door

Bewijs dat geen enkel getal van de vorm

    \[3^m+3^n+1\]

met m en n strikt positieve gehele getallen, een volkomen kwadraat is.

Antwoord

  • Veronderstel dat er toch een natuurlijk getal k bestaat zodat

        \[3^3+3^n+2=k^2\]

  • Dan is 3^m+3^n=(k+1)(k-1). Omdat het linkerlid even is en omdat k-1 en k+1 dezelfde pariteit hebben, zijn k-1 en k+1 opeenvolgende even getallen.
  • Dit betekent ook dat ofwel k-1 ofwel k+1 een viervoud is. Het rechterlid (k-1)(k+1) is dus deelbaar door 8.
  • Bij deling door 8 zijn de resten van machten van 3 ofwel 1 ofwel 3. De som 3^m+3^n is dus modulo 8, gelijk aan 2,4 of 6 en dus zeker niet deelbaar door 8.
  • Bijgevolg kan 3^m+3^n+1 nooit een volkomen kwadraat zijn.

Opgave 38

Geplaatst op door

Antwoord

  • Bekijken we het probleem wat algemener en gebruiken we de eigenschap dat de raaklijnen vanuit een punt aan een cirkel evenleng zijn.
  • Noteren we de straal van de ingeschreven cirkel met x .
  • We passen  nu de stelling van Pythagoras toe: 5^ 2=(x+2)^2+(x+3)^2.
  • Deze vierkantsvergelijking heeft als oplossing 1 en -6. Bijgevolg is x=1.
  • De gevraagde oppervlakte is dan \frac{1}{2}(2+1)(3+1)=6.