Het is voor iedereen duidelijk dat een kwadraat van een reeël getal nooit negatief kan zijn. Het uitwerken van ![]() geeft ons twee eenvoudige ongelijkheden, waarmee we snel aan het werk kunnen ( veronderstel alle getallen positief):
geeft ons twee eenvoudige ongelijkheden, waarmee we snel aan het werk kunnen ( veronderstel alle getallen positief):
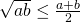 .
. .
.
Twee voorbeelden:
- Bewijs dat
 .
.
Uit formule 1 vinden we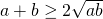 , maar ook dat
, maar ook dat  en
en  , dus is
, dus is  .
. - Bewijs, als
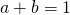 , dan is
, dan is  .
.
Uit formule 2 volgt het linkerlid groter is dan of gelijk is aan . Uit formule 1 weten we dat
. Uit formule 1 weten we dat 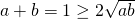 ofwel
ofwel  . Hieruit volgt dat
. Hieruit volgt dat 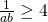 .
.
Bijgevolg is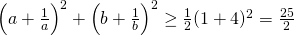 .
.
