Peter is een geheim agent die gevangen gehouden wordt door terroristen Hij heeft een ontsnappingsplan: volg de kwadratische vergelijking , waarbij de vloer van zijn kamer als het complexe vlak wordt bekeken en waar hij in de oorsprong staat.  Peter kent echter de constante c niet. Voor welke waarden van c heeft hij een kans op ontsnapping?

Proberen we eerst c = 0. Maar dan wordt, voor elke n, en blijft hij steeds op dezelfde plaats. Als we andere waarden van c proberen, zijn er 3 mogelijkheden:

1. De rij 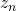convergeert naar een vast punt.
2. De rij 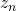wordt herhaald in een eindige cyclus van punten en wordt een periodieke rij.
3. De rij 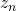divergeert weg van de oorsprong en Peter heeft kans op ontsnapping.

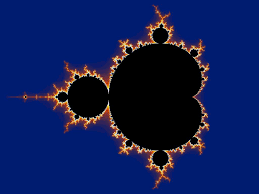
Dit verhaal is eigenlijk het verhaal van de Mandelbrot verzameling, namelijk de verzameling van alle complexe getallen c waarvoor de baan van begrensd is ( dus niet divergeert) met startpunt .