Wanneer deelt een natuurlijk getal n de uitdrukking 
voor een natuurlijke k?
Spoiler
- Als n een veelvoud is van 2 of 5, dan is de enige mogelijkheid de triviale oplossing k=0.
- Veronderstel dus verder dat n geen priemfactor 2 of 5 bevat.
- Noteer met K(n) de kleinste, van 0 verschillende waarde van k, waarvoor
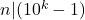. - Proberen we een aantal waarden uit:
- Stel nu dat n, geen priemfactor 2 of 5 bevat, en een deler is van 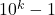, dan bestaat er een natuurlijk getal a zodat
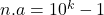. - Noteer de decimale schrijfwijze van a als
. - Dan is
. - Bij deling, van deze laatste vergelijking door
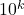vinden we: ![\[0,a_1\cdots a_{k-1}a_k=\frac{1}{n}-\frac{10^{-k}}{n}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-91aba792e511039f2c73533a98fd9cbd_l3.png?media=1678572382 "Rendered by QuickLaTeX.com")
- Als we steeds maar opnieuw delen door 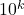en alle bekomen formules lid per lid bij elkaar optellen vinden we
![\[\frac{1}{n}=0,a_1\cdots a_{k-1}a_ka_1\cdots a_{k-1}a_k\cdots\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-ed90fadd64ccfc2d40ea0bd5e380b1a1_l3.png?media=1678572382 "Rendered by QuickLaTeX.com")
- Omgekeerd is het eenvoudig te zien dat, als
een decimale ontwikkeling zoals hierboven heeft, dat n een deler is van 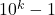. - Besluit: Als n geen priemfactor 2 of 5 bevat, dan in K(n) gelijk aan de lengte van de periode van .
- Natuurlijk is elk veelvoud van k ook een goede oplossing.