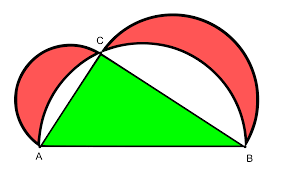
Antwoord
- De groene oppervlakte is gelijk aan de rode oppervlakte.
- We duiden volgende gebieden aan en noteren de schuine zijde van de gele rechthoekige driehoek a en de rechthoekszijden b en c:
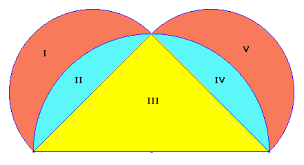
- Te bewijzen is dat I + V = III
- De stellig van Pythagoras zegt:
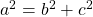. - Na deling door 8 en vermenigvuldiging met
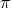geeft dit: ![\[\frac{1}{2}\pi \Big( \frac{a}{2} \Big)^2=\frac{1}{2}\pi \Big( \frac{b}{2} \Big)^2+\frac{1}{2}\pi \Big( \frac{c}{2} \Big)^2\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-d261dbf7382edbd278a85b8ddc273caf_l3.png?media=1678572382 "Rendered by QuickLaTeX.com")
- Vertaald naar oppervlaktes van halve cirkels geeft dit : II + III + IV = I +II +IV +V of na vereenvoudiging: I + V = III
- Deze figuur noemt men ook wel eens de maantjes van Hippocrates. Ze wordt toegeschreven aan de Griekse wiskundige Hippocrates van Chios (rond 430 voor Christus).