Tag archieven: Pythagoras

Nootje 41

Geplaatst op door

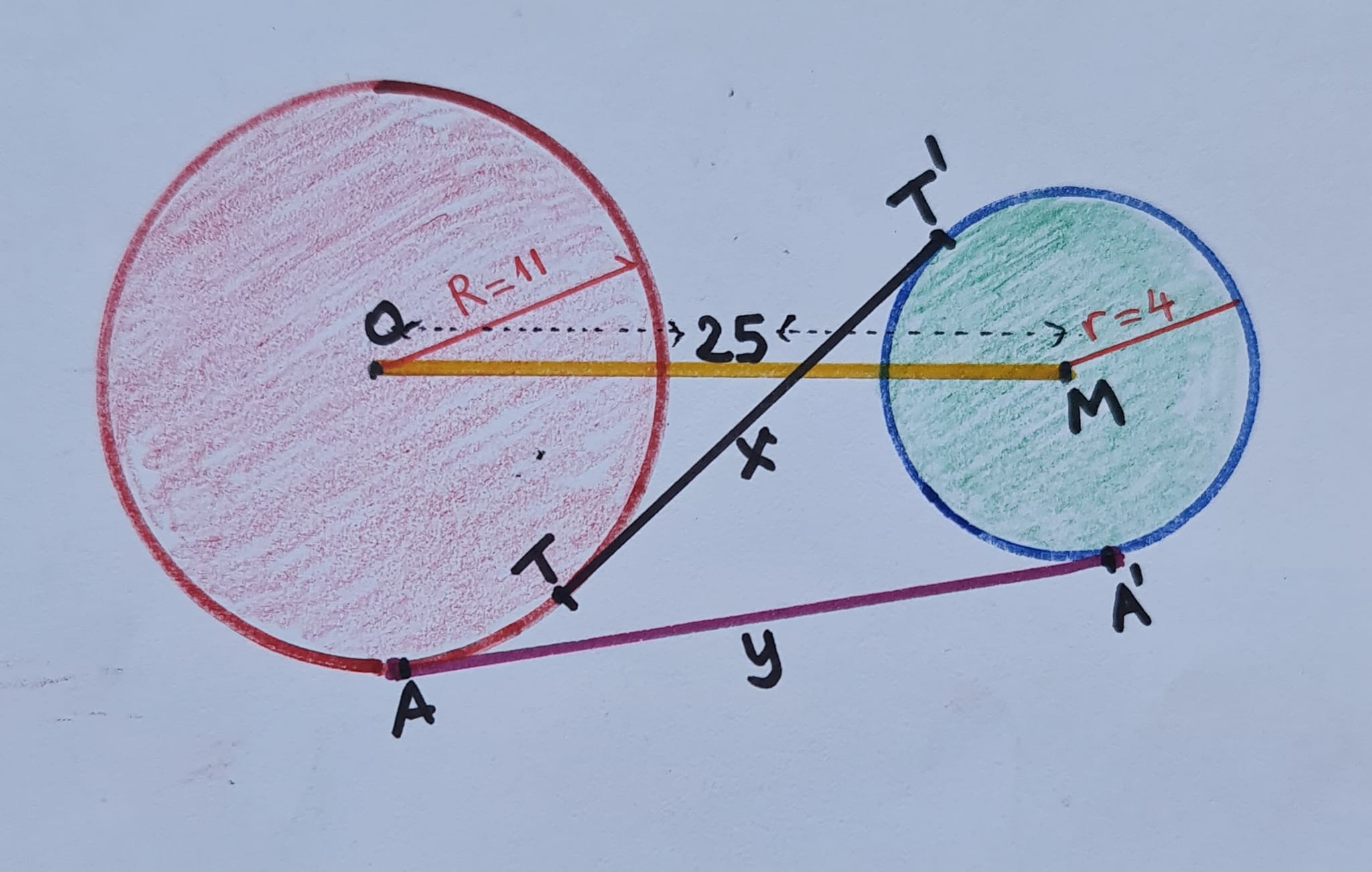
Gegeven zijn twee cirkels met stralen 4 en 11. De afstand tussen hun middelpunten is 25. Bepaal de som van de lengtes van een inwendig en een uitwendig  gemeenschappelijke raaklijn.

Antwoord

  • Verbind de middelpunten van de cirkels met de raakpunten A en A’ en teken door A’ een evenwijdige met de rechte die de middelpunten van de twee cirkels (de centraal)  verbindt.
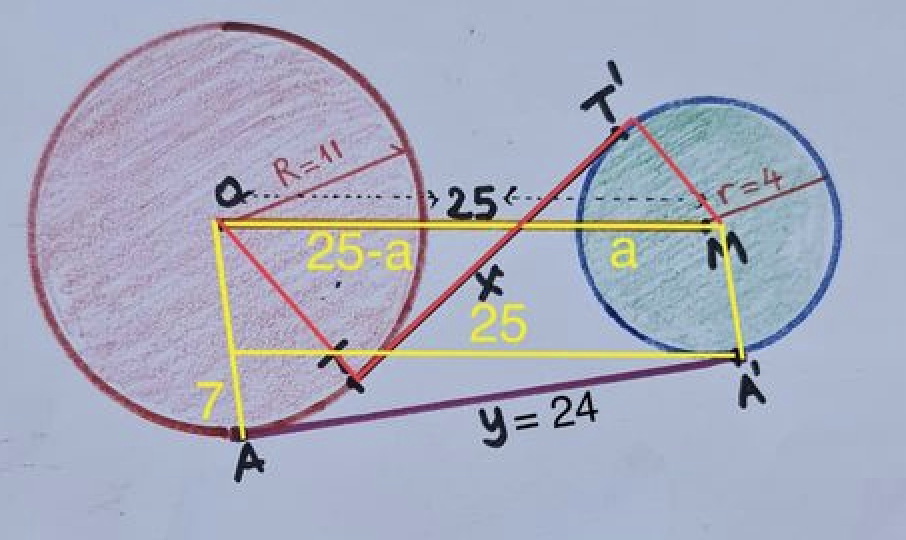
  • De onderste driehoek is rechthoekig. De schuine zijde meet 25 en één van de rechthoekszijden is 11-4=7. Dus is, volgens Pythagoras y=24.
  • Noteer met S het snijpunt van de centraal met TT’.
  • De driehoeken OTS en MT’S zijn gelijkvormige rechthoekige driehoeken. Dus \frac{25-a}{11}=\frac{a}{4}. Bijgevolg is a=\frac{20}{3}.
  • Dan is x=|TS|+|T'S|=\sqrt{a^2-4^2}+\sqrt{(25-a)^2-11^2}=20.
  • Tenslotte is de gevraagde som gelijk aan x+y=44.

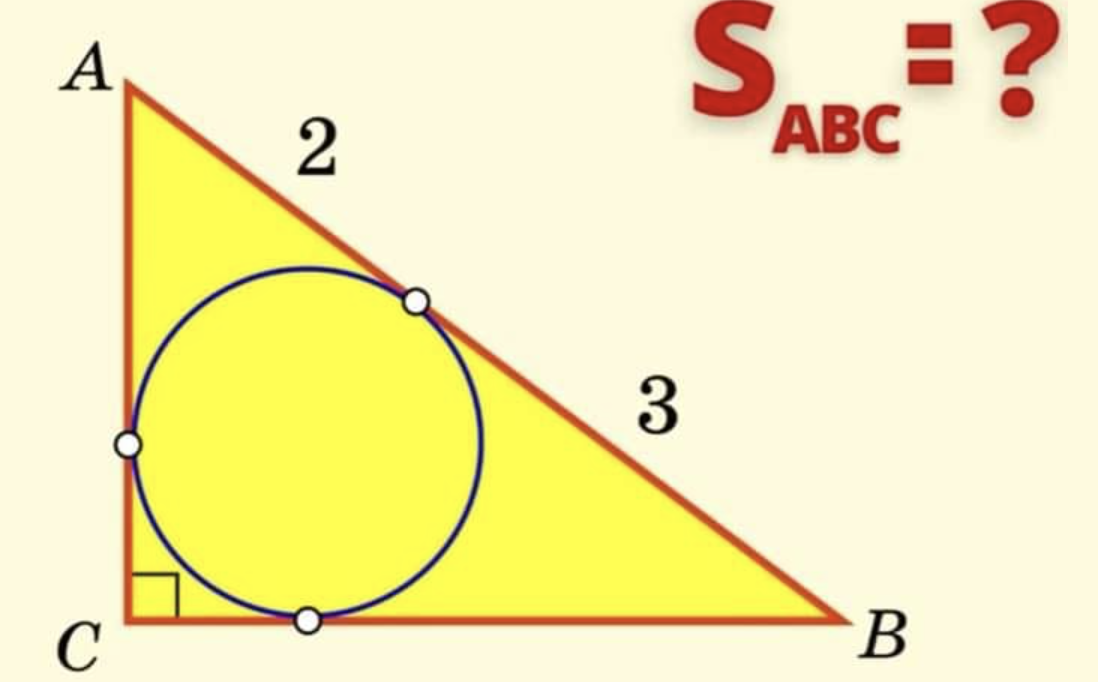
Opgave 38

Geplaatst op door

Antwoord

  • Bekijken we het probleem wat algemener en gebruiken we de eigenschap dat de raaklijnen vanuit een punt aan een cirkel evenleng zijn.
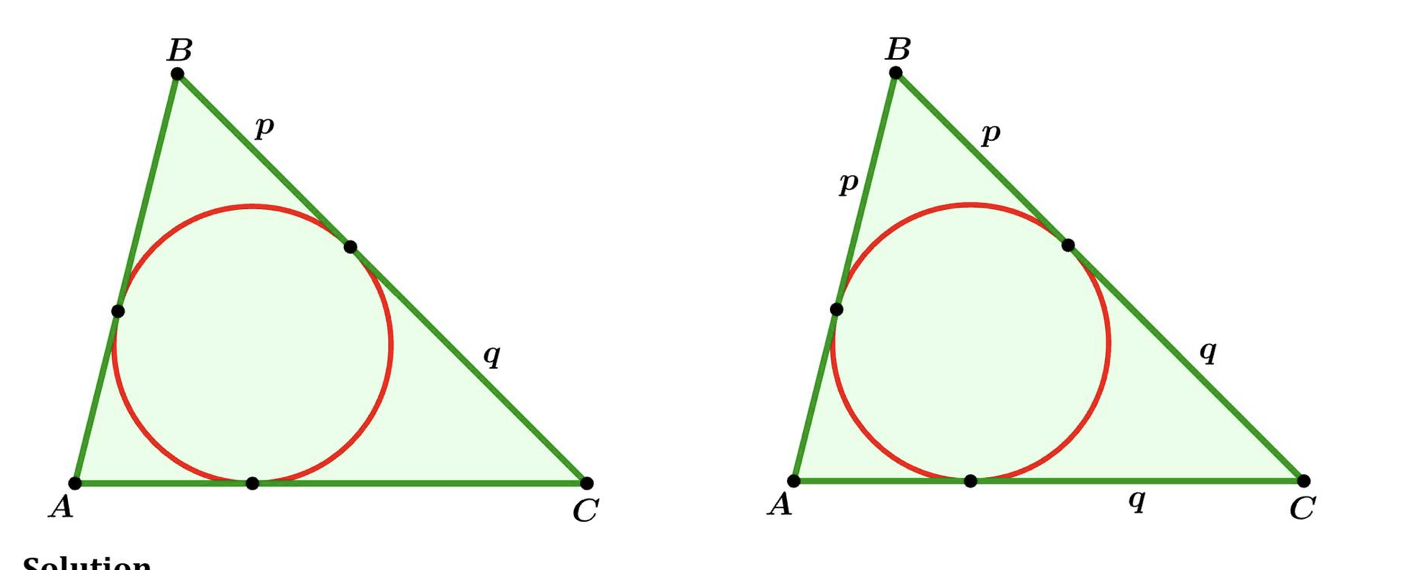
  • Noteren we de straal van de ingeschreven cirkel met x .
  • We passen  nu de stelling van Pythagoras toe: 5^ 2=(x+2)^2+(x+3)^2.
  • Deze vierkantsvergelijking heeft als oplossing 1 en 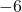-6. Bijgevolg is x=1.
  • De gevraagde oppervlakte is dan \frac{1}{2}(2+1)(3+1)=6.

Sangaku 11

Geplaatst op door

Antwoord

  • De bedoeling is de oppervlakte van het vierkant te bepalen.
  • De horizontale rechthoekzijde van de rode driehoek is gelijk aan \sqrt{27}-\sqrt{12}=\sqrt{3}. De andere rechthoekszijde meet \sqrt{12}=2\sqrt{3} en is dus dubbel zo groot als de horizontale rechthoekzijde.
  • De zwarte driehoek is gelijkvormig met de rode en omdat de verticale rechthoekzijde gelijk is aan \sqrt{3}+\sqrt{12}+\sqrt{27}=6\sqrt{3}, moet de horizontale rechthoekzijde gelijk zijn aan de helft ervan , dus 3\sqrt{3}.
  • Volgens de stelling van Pythagoras is het kwadraat van de zijde van het vierkant dan gelijk aan (6\sqrt{3})^2+(3\sqrt{3})^2=135
  • De gevraagde oppervlakte is dus 135.