Om een probleem op te lossen verzamelen we eerst alle gegevens. We proberen ze te begrijpen en te analyseren. Maar soms kunnen we dat niet doen op een betekenisvolle manier omdat de berekeningen te ingewikkeld zijn of omdat er bijvoorbeeld geen speciale gevallen zijn die ons enig inzicht kunnen geven in het probleem. We proberen dan het probleem te herformuleren in een equivalente maar eenvoudiger vorm. Hiervoor zullen we gebruik moeten maken van onze verbeelding en creativiteit. Dikwijls gebruiken we hiervoor algebraïsche of goniometrische formules, substitutie of verandering van onbekende,…
Voorbeeld:
Vind een algemene formule voor de n-de afgeleide van
![]()
 ,
,  ,
,  . De uitdrukking wordt steeds ingewikkelder en we zien geen regelmaat verschijnen.
. De uitdrukking wordt steeds ingewikkelder en we zien geen regelmaat verschijnen.- Misschien kunnen we de opgave eerst vereenvoudigen en dan denken we onmiddellijk aan splitsen in partieelbreuken:
![Rendered by QuickLaTeX.com \[f(x)=\dfrac{1}{2}\Big(\dfrac{1}{1-x}+\dfrac{1}{1+x}\Big)\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-b1ed31df0a83740c8ae88f8664fc48da_l3.png?media=1678572382)
- Het probleem is nu herleid tot het vinden van een algemene formule voor de n-de afgeleide van
 en
en  .
.  ,
, 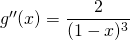 ,
,  . Zo komen we tot de formule:
. Zo komen we tot de formule:
![Rendered by QuickLaTeX.com \[g^{n}(x)=\dfrac{n!}{(1-x)^{n+1}}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-757f8c0f6755eab80b3c65393bb775bb_l3.png?media=1678572382)
We kunnen dit eventueel bewijzen via inductie.
- Analoog vinden we :
![Rendered by QuickLaTeX.com \[h^n(x)=\dfrac{(-1)^n.n!}{(1+x)^{n+1}}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-50d1f5845d5e15c63978f0ec0641837c_l3.png?media=1678572382)
- We besluiten dus:
![Rendered by QuickLaTeX.com \[f^n(x)=\dfrac{n!}{2}\Big(\dfrac{1}{(1-x)^{n+1}}+\dfrac{(-1)^n}{(1+x)^{n+1}}\Big)\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-58df4c785e74f63d23430b2a9adb1045_l3.png?media=1678572382)

