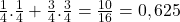Bereken de kans dat de determinant van een 2×2 matrix, met natuurlijke getallen als elementen,  even is.

• Gegeven een matrix .
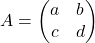• Zijn determinant is

     

• Een product van twee natuurlijke getallen is oneven als beide getallen oneven zijn, dus de kans dat 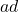oneven is, is . De kans dat 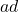even is, wordt dat .
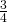• Nu is 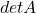even als 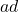en 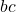beiden even zijn of beide oneven zijn.
• De kans dat 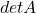even is , is bijgevolg gelijk aan