AB is een koorde en P een willekeurig punt van een gegeven cirkel. Q is de loodrechte projectie van P op AB en R en S zijn de loodrechte projecties van P op de raaklijnen aan de cirkel in A en B. Bewijs dat PQ het meetkundig gemiddelde is van PR en PS.
Antwoord
- Maken we eerst een tekening:
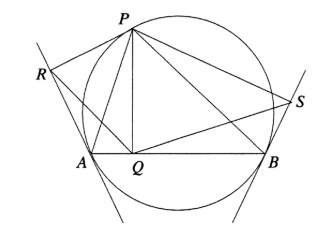
- We proberen aan te tonen dat de driehoeken PRQ en PQS gelijkvormig zijn, want dan is
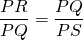 en hieruit volgt het gestelde.
en hieruit volgt het gestelde. - De vierhoeken PRAQ en PQSB zijn koordenvierhoeken omdat twee overstaande hoeken recht zijn.
- In de eerste koordenvierhoek is
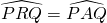 omdat in een koordenvierhoek de hoek tussen een zijde en de diagonaal gelijk is aan de hoek gevormd door de overstaande zijde en de andere diagonaal. Daarom is ook
omdat in een koordenvierhoek de hoek tussen een zijde en de diagonaal gelijk is aan de hoek gevormd door de overstaande zijde en de andere diagonaal. Daarom is ook  .
. - Maar de hoeken
 en
en  zijn gelijk als hoeken op eenzelfde boog in de gegeven cirkel. Bijgevolg is
zijn gelijk als hoeken op eenzelfde boog in de gegeven cirkel. Bijgevolg is 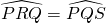 .
. - Via een analoge redenering is ook
 en dus zijn de driehoeken PRQ en PQS gelijkvormig, zoals gevraagd.
en dus zijn de driehoeken PRQ en PQS gelijkvormig, zoals gevraagd.
