Gegeven: 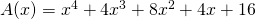 . Zoek alle getallen x waarvoor
. Zoek alle getallen x waarvoor  een volkomen kwadraat is.
een volkomen kwadraat is.
Antwoord
- Het is duidelijk dat
 een volkomen kwadraat is. Zijn er nog andere mogelijkheden?
een volkomen kwadraat is. Zijn er nog andere mogelijkheden?  lijkt op
lijkt op  : namelijk
: namelijk  . Met andere woorden
. Met andere woorden  is zeker groter dan
is zeker groter dan 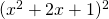 .
.- Neem
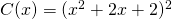 . Wil
. Wil 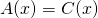 dan moet
dan moet  of
of  .
. - Neem
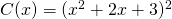 . Wil
. Wil 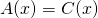 dan moet
dan moet 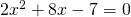 . Dit heeft geen gehele oplossingen.
. Dit heeft geen gehele oplossingen. - Neem
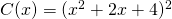 . Wil
. Wil 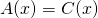 dan moet
dan moet  . Bijgevolg is
. Bijgevolg is 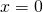 of
of 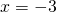 .
. - Neem
 . Wil
. Wil 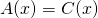 dan moet
dan moet  en hier zijn geen gehele oplossingen mogelijk.
en hier zijn geen gehele oplossingen mogelijk. - Neem
 . Dan is
. Dan is 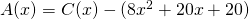 . Hieruit volgt dat
. Hieruit volgt dat  en dus stopt ons onderzoek hier.
en dus stopt ons onderzoek hier. - De enige oplossingen zijn 0,3,-3. Hierbij is
 ,
, 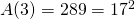 en
en 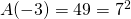 .
. - Gelukkig kunnen we
 naar boven begrenzen, anders zou het proces oneindig lang verdergaan.
naar boven begrenzen, anders zou het proces oneindig lang verdergaan.
