Cissoïde van Diocles | Wiskunde is leuk

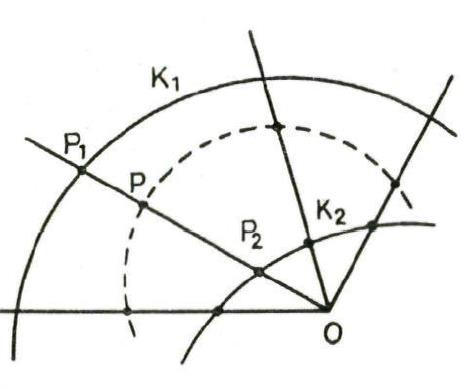
Gegeven zijn een kromme $K_1$ en $K_2$ en een punt O. Door O trekt men een rechte die $K_1$ snijdt in $P_1$ en $K_2$ in $P_2$ . Op die rechte bepaalt men een punt P zodat $|OP|=|OP_1|-|OP_2|$ . Wanneer men de rechte nu laat draaien rond O, is de meetkundige plaats van de punten P een cissoïde(afkomstige uit het Grieks: kimos = klimop).

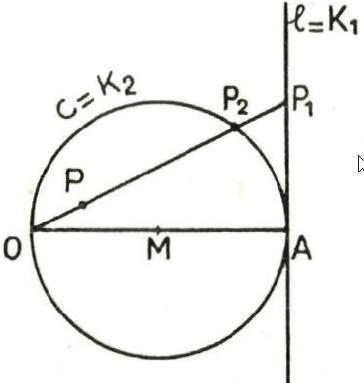
De cissoïde van Diocles verkrijgt men als $K_1$ een rechte is die raakt in een punt A aan een cirkel ( $K_2$ ). Voor O neem je het punt op de cirkel diametraal tegenover A.

Neem O als oorsprong van het assenstelsel en de rechte OA als X-as. Veronderstel dat de straal van de cirkel gelijk is aan a. De cirkel heeft als vergelijking $(x-a)^2+y^2=a^2$ en de raaklijn heeft als vergelijking $x=2a$ . Een willekeurige rechte door O kunnen we voorstellen door $y=\lambda x$ . Dan is $P_1(2a,2a\lambda)$ en $P_2(\dfrac{2a}{1+\lambda^2},\dfrac{2a\lambda}{1+\lambda^2})$ . Om de meetkundige plaats te vinden van de punten P, als de rechte rond O draait, moeten we $\lambda$ elimineren uit $y=\lambda x$ en uit $x=2a-\dfrac{2a}{1+\lambda^2}$ . Deze laatste voorwaarde bekomen we door de voorwaarde $|OP|=|P_1P_2|$ te projecteren op de X-as. Als resultaat krijgen we

$x(x^2+y^2)=2ay^2$

In Geogebra: