Categorie archieven: Kleine nootjes

Nootje 53

Geplaatst op door

De eerste prijs, in Euro’s, bij een loterij is een getal van 5 cijfers. Nina en 3 van haar vrienden winnen de prijs en verdelen die in gelijke delen onder elkaar. Nina merkt dat haar deel dezelfde cijfers heeft als de totale prijs, maar dan in omgekeerde volgorde. Hoe groot is Nina’s deel?`

Antwoord

  • stel de totale prijs door abcde.
  • er geldt dan dat abcde= 4.edcba.
  • Omdat 4e<10 moet e=1 of e=2.Omdat 4a eindigt op cijfer e, moet e dus even zijn en dus is e=2
  • nu e=2, eindigt 4a op een 2 en dus is a=3 of 8.
  •  We weten dat e=2,718 dus is a\geq 8 en dus is a=8.
  • We hebben dus al dat 8bcd2=4. 2dcb8
  • Volledig uitgeschreven: 80000+1000b+100c+10d+2=80000+4000d+400c+40b+32
  • Dit wordt dan: 960b=300c+3990d+30 of na vereenvoudiging 32b=10c+133d+1
  • Kijkend neer even en oneven vinden we dat 133d+1 even moet zijn en dus id d oneven. Anderzijds is 32 b > 133d, dus zeker 32b>128d of b>4d. gecombineerd met het oneven zijn van d, volgt hieruit dat d=1.
  • De vergelijking,g twee stappen terug wordt dan 32b=10c+134.
  • 32b moet dus op een 4 eindigen en omdat b>4, weten we dat b=7
  • We bekomen tenslotte 224=10c+134 of c=9
  • Het deel van Nina is dus 21978 Euro

Nootje 51

Geplaatst op door

20 leerlingen van een zelfde klas versturen  in december elk 10 wenskaarten naar 10 verschillende klasgenoten. Toon aan dat er minstens twee leerlingen zijn die een kaart naar elkaar sturen.

“Antwoord“

  • Dit doet me denken aan het duivenhokprincipe of principe van Dirichlet:  Wanneer n + 1 duiven in n hokken neerstrijken, dan is er altijd minstens 1 hok met minstens twee duiven.
  • De hokken zijn de koppels leerlingen: hiervoor moet je het aantal 2-combinnatir nemen van 20 elementen en dat is \binom{20}{2}=190.
  • De duiven zijn de brieven: zo zijn er 20*10=200
  • Bijgevolg heeft minstens 1 koppel twee brieven en zijn er dus zeker twee leerlingen die aan elkaar geschreven hebben.

Nootje 49

Geplaatst op door

De functie f is gedefinieerd op de verzameling geordende paren positieve getallen en voldoet aan :f(x,x)=x , f(x,y)=f(y,x) en f(x,y).(x+y)=y.f(x,x+y). Bereken f(14,52)

Antwoord

  • f(14,52)=f(14,14+38). Pas nu regel 3 toe:
  • f(12,52)=\frac{52}{38}f(14,38). Nu is 38=14+24. Pas opnieuw regel 3 toe en we krijgen:
  • f(12,52)=\frac{52}{24}f(14,14+10). Nogmaals regel 3:
  • f(12,52)=\frac{52}{10}f(14,10)
  • We draaien de argumenten om volgens regel 2 en we vinden 
  • f(12,52)=\frac{52}{10}f(10,14)
  • f(12,52)=\frac{52}{10}f(10,10+4)=\frac{52}{10}.\frac{14}{4}.f(10,4)
  • Omdraaien : f(12,52)=\frac{91}{5}.f(4,4+6)=\frac{91}{3}.f(4,4+2)
  • Nog maar een keer regel 3 geeft :f(12,52)=91.f(4,2)=91.f(2,2+2).
  • Uiteindelijk bekomen door regel 3 en regel 1 het antwoord:

        \[f(14,52)=91.2.f(2,2)=91.2.2=364\]

 

Nootje 48

Geplaatst op door

Bepaal alle drietallen natuurlijke getallen a,b,c waarvoor a.b.c=1989 en a+b+c=89

Antwoord

  • De oplossing is symmetrisch in a,b en c.
  • Redeneren we eventjes op c, dan moet c moet een deler zijn van 1989=3^2.13.17.
  • De delers van 1989 zijn: 1,3,9,13,17,39,51,117,153,221,663,1989.
  • Bij een keuze van c moeten we nog het stelsel oplossen:

        \[\begin{cases}a+b=89-c \\ a.b=\frac{1989}{c}\end{cases}\]

  • Noteer S=a+b en P=a.b, dan zijn a en b oplossingen van de vergelijking

        \[x^2-Sx+P=0\]

  • S=89+c; Omdat c oneven is , zal S dus even zijn en moet de discriminant S^2-4P een kwadraat zijn van een even getal ( anders zijn a en b geen natuurlijke getallen).
  • Voor 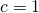c=1 is S=90 en P=1989. In dat geval is de discriminant gelijk aan 144 en vinden we dat a=39 en b=51.
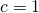  • Voor c=1 krijgen we dus als oplossingen de drietallen (39,51,1) en (51,39,1). 
  • Door de symmetrie zijn de andere oplossingen dan (1,39,51),(1,51,39),(39,1,51),(51,1,39).