Categorie archieven: Getaltheorie

Priemgetallen

Geplaatst op door

De Poolse wiskundige W.Sierpinski (1882-1969) was eer gefascineerd door de priemgetallen en hun spreiding tussen de andere natuurlijke getallen. We vermelden twee mooie resultaten.

Men kan een rij van opeenvolgende natuurlijke getallen bepalen, zo lang als men wilt, die geen enkel priemgetal bevat. Zo kan men bijvoorbeeld 100 opeenvolgende getallen kiezen zonder dat er een priemgetal inzit.  Neem 101!+2,101!+3,…,101!+101. Dit zijn 100 opeenvolgende getallen en ze zijn geen van allen priem want ze zijn respectievelijk deelbaar door 2,3,…,101

Voor elke n kan men een priemgetal vinden met links en rechts ervan n niet-priemen:

  • Neem een priemgetal q groter dan n+1.
  • Bereken a=\prod_{j=1}^{q-2}(q^2-j^2).
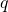  • q  is onderling ondeelbaar met a.
  • De stelling van Lejeune-Dirichlet over de rekenkundige rij zegt dat er een priemgetal p bestaat met p>q en p=ak+q.
  • Nu is q+j een deler van a en omdat p+j=ak+q+j ook een deler van p+j. 
  • Analoog is q-j een deler van p-j.
  • Dus zijn p-j en p+j niet priem en dit voor j=1,2,…,n

Neem n=2 en q respectievelijk de priemgetallen 5,7,11,13,…, dan kan je zo bewijzen dat er oneindig veel priemgetallen bestaan die geen deel uitmaken van een priemtweeling.

Stapel permutaties

Geplaatst op door

Een stapel register kan eenvoudig voorgeteld worden als een systeem met een  ingang(I) en een uitgang (U) met daartussen een wachtplaats( stapel of stack):

Neem de rij 123  en voer de volgende instructies uit: 3 in de stapel, 2 in de stapel, 2 uit de stapel, 1 in de stapel, 1 uit de stapel, 3 uit de stapel . De rij cijfers die aan de uitgang verschijnt is dan 213.

We zeggen dat 213 een stapelpermutatie is, omdat ze met een eindig aantal in en uit bewegingen kan bekomen worden  van de oorspronkelijke  rij 123. Van de zes ‘gewone’ permutaties van 123 is enkel 231 geen stapelpermutatie. Er zijn dus 5 stapelpermutaties van de rij 123.

Zijn er n elementen gegeven, dan is het aantal stapelpermutaties gegeven door

    \[cat(n)=\binom{2n}{n}-\binom{2n}{n-1}\]

Dit getal noemen we het n-de Catalangetal. We spreken ook af dat cat(0)=1. De eerste Catalaanse getallen zijn: cat(1)=1,cat(2)=2,cat(3)=5,cat(4)=14,cat(5)=42.

De naamgeving verwijst naar de Belgische wiskundige Eugene Catalan (Brugge 1814-Luik 1894). Catalaanse getallen vormen een fascinerende rij in de wiskunde, bekend om hun talrijke verschijningen in verschillende combinatorische problemen. Catalaanse getallen zijn een voorbeeld van hoe wiskundige structuren en patronen op onverwachte manieren kunnen opduiken. Een paar voorbeelden:

Een Dyck-pad van lengte 2n is een pad in een rooster dat niet onder de diagonaal komt en van naar loopt. Het aantal van dergelijke paden wordt gegeven door cat(n).

Het aantal manieren om een convexe -hoek op te splitsen in driehoeken met niet-overlappende diagonalen is gelijk aan cat(n).

Het aantal manieren om 2n punten op een cirkelomtrek te verbinden met koorden die elkaar niet snijden is cat(n).

 

 

Les 5: Diophantische vergelijkingen en modulo rekenen

Geplaatst op door

Als twee gehele getallen gelijk zijn, dan zijn hun resten bij deling door een zelfde natuurlijk getal, verschillend van nul, ook gelijk. Of via contrapositie: als er tenminste 1 natuurlijk getal n bestaat waarvoor a \neq b \mod n, dan zal ook a verschillend zijn van b.

Proberen we eens met

    \[2x^2-3y^2-9463=0\]

  • Herschrijf tot 2x^2-3y^2=9463.
  • We bepalen de resten van beide leden bij deling door 3: 2x^2-3y^2\equiv 9463 \mod 3.
  • Of 2x^2\equiv 1 \mod 3.
  • Het inverse element, modulo 3, van 2 is 2 zelf, dus kunnen we vorige  vergelijking herschrijven als

        \[x^2\equiv 2 \mod 3\]

  • Nu is 2 geen kwadraatrest modulo 3, want 0^2=0,1^2=1 en 2^2=1.
  • Bijgevolg heeft de gegeven vergelijking geen oplossingen.

Les 4: ontbinding en exhaustie

Geplaatst op door

Bij Diophantische vergelijkingen van een hogere graad kan je via ontbinding in factoren dikwijls de oplossing vinden. Neem bijvoorbeeld:

    \[3x^2-4xy+5=0\]

  • We kunnen deze vergelijking herschrijven als

        \[x(3x-4y)=-5\]

  • Als x en y gehele getallen zijn, dan moeten x en 3x-4y delers zijn van -5.
  • We kunnen gemakkelijk alle mogelijkheden opschrijven: 

        \[\begin{array}{c|c|c} x&3x-4y&y \\ \hline \\1&-5&2\\-1&5&-2\\5&-1&4\\-5&1&-4\end{array}\]

  • We hebben dus als oplossingen (1,2),(-1,-2),(5,4),(-5,-4).

 

Les 3: Stelsels Diophantische vergelijkingen

Geplaatst op door

We lossen één van de vergelijkingen op en vullend die dan in de andere in, waardoor er een verband ontstaat tussen de parameters. Neem bijvoorbeeld:

    \[\left\{\begin{matrix} 3x-6y+16z=1\\2x+5y-6z=2\end{matrix}\right\]

  • Uit les 2 weten we dat de oplossing van de eerste vergelijking gegeven wordt door  x=5+16t+2v, y=5+16t+v, z=1+3t.
  • Invullen in de tweede vergelijking geeft: 2(5+16t+2v)+5(5+16t+v)-6(1+3t)=2. Na uitwerking vinden we 94t+9v=-27.
  • Dit is een Diophantische vergelijking met slechts twee onbekenden. De oplossingen hangen af van 1 parameter w: t=54-9w en v=-567+94w.
  • Brengen we deze waarden in bij de oplossingen van de eerste vergelijking van het stelsel, dan vinden we :

        \[\left\{\begin{matrix}x=-265+44w\\y=302-50w\\z=163-27w\end{matrix}\right\]