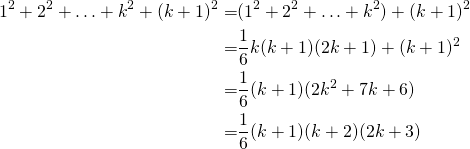n spelers spelen n spelen en winnen om de beurt. Telkens een speler wint, verdubbelt hij het bezit van zijn n-1 tegenspelers. Op het einde hebben ze allemaal evenveel. Hoeveel hadden ze in het begin?
- Laten we eenvoudig beginnen met 3 spelers, die in het begin a,b en c bezitten. Het rijtje tussen resultaten van de eerste speler is (a, a-b-c,2(a-b-c),4(a-b-c)). Het rijtje voor de tweede speler is (b,2b,3b-a-c,2(3b-a-c)). tenslotte voor de derde speler (c,2c,4c,7c-a-b). Als ze allemaal evenveel hebben op het laatst dan moet 4(a-b-c)=2(3b-a-c)=7c-a-b.. Dit stelsels is gelijkwaardig met : 4b=7c en 4a=13c. Hieruit volgt dat a=13, b=7 en c=4.
- Deze manier van werken wordt moeilijk voor willekeurige n.
- Noteer met s het totaal bezit van alle spelers. Op het einde hebben ze dan allemaal
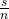 .
. - Na het eerste spel heeft de eerste speler
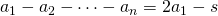 .
. - Al de volgende keren wordt zijn bedrag verdubbeld zodat hij op het einde
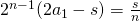 heeft. Hieruit volgt dat
heeft. Hieruit volgt dat 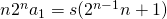 .
. - Een analoge redenering voor speler 2 geeft :
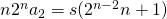 . Idem voor alle andere spelers.
. Idem voor alle andere spelers. - Hieruit volgt dat ze allen op het einde
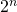 bezitten en dat in het begin speler k een som van
bezitten en dat in het begin speler k een som van 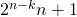 heeft
heeft