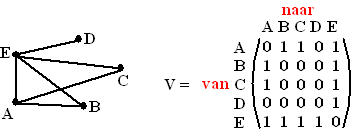Categorie archieven: Discrete wiskunde

Euler circuit

Geplaatst op door

Een Eulerpad in een graaf is een pad waarbij elke lijn juist 1 keer wordt aangedaan.

We spreken van een Eulercircuit als bovendien vertrekpunt en eindpunt van het pad dezelfde zijn. Bvb 4 3 0 1 2 0 4

Het was Euler die volgende stelling over Eulercircuits bewezen heeft:

Een samenhangende graaf heeft een Eulercircuit als en slechts als elk punt van de graaf een even graad heeft.

Kijk maar naar de graden in  volgend voorbeeld:

Ook het probleem van de bruggen van Koningsberg is hiermee opgelost. Alle punten van de graaf hebben graad 3 en bijgevolg is een route langsheen de vier bruggen, waarbij elke brug precies één keer bewandeld wordt en waarbij men terugkeert naar de startplaats, niet te vinden.

36 officieren

Geplaatst op door

Het 36 officieren probleem, ook wel bekend als het probleem van Euler’s 36 officieren, is een beroemde puzzel in de combinatoriek, bedacht door de wiskundige Leonhard Euler in 1782. Het probleem kan als volgt worden omschreven:

Stel je hebt een leger van 36 officieren, bestaande uit 6 verschillende regimenten en 6 verschillende rangen. Je moet deze 36 officieren opstellen in een 6×6 rooster, zodanig dat in elke rij en elke kolom precies één officier van elk regiment en één officier van elke rang voorkomt.

Euler conjectureerde dat dit probleem geen oplossing heeft voor een 6×6 rooster, en dit werd later bewezen door Gaston Tarry (1843-1913) in 1901. Het betekent dat het onmogelijk is om een 6×6 rooster te vullen met deze eigenschappen. De onmogelijkheid van het oplossen van het 36-officieren probleem komt voort uit het feit dat het een speciaal geval is van het algemene probleem van het vinden van “orthogonale Latijnse vierkanten”. Latijnse vierkanten zijn roosters waarbij in elke rij en kolom elke symbool precies één keer voorkomt. Twee Latijnse vierkanten zijn orthogonaal als je ze over elkaar legt en elke combinatie van symbolen precies één keer voorkomt. Voor n=6 bestaat er geen paar van orthogonale Latijnse vierkanten, wat het 36-officieren probleem onoplosbaar maakt.

Euler vermoedde dat als n=4k+2, waarbij k een natuurlijk getal is, er geen paar orthogonale Latijnse vierkanten van n\times n bestaat. Dit vermoeden werd pas in 1959 ontkracht, toen de wiskundigen Bose,Shikhande en Parker een paar orthogonale Latijnse vierkanten van 22 \times 22 maakten. 

Er bestaan wel oplossingen als bijvoorbeeld  n=5 en n=7

 

 

Vrijdag de dertiende

Geplaatst op door

 

Toon aan dat er in ieder jaar minstens 1  en hoogstens 3 keer vrijdag de dertiende   voorkomt.

  • De dertiende van elke maand in een niet-schrikkeljaar hebben als dagnummer:13,44,72,103,133,164,194,225,256,286,317,347.
  • De resten bij deling door 7 zijn: 6,2,2,5,0,3,5,1,4,6,2,4
  • Twee maanden A en B worden in hetzelfde vakje geplaatst als de dertiende van die maanden op dezelfde dag van de week vallen. Omdat elk getal, van 0 tot 6, voorkomt in de laatste rij, zijn de maanden over de 7 vakjes verdeeld.
  • Elk van de 7 vakjes stelt één van de dagen van de week voor. Omdat elk vakje bezet is, komt er minstens 1 vrijdag de dertiende voor in een niet-schrikkeljaar.
  • Een zelfde waarde in dat rijtje resten komt hoogstens 3 maal voor, dus kunnen er hoogstens 3 vrijdagen de dertiende voorkomen.
  • Voor een schrikkeljaar zijn de dagnummers van de dertiende: 13,44,73,104,134,165,195,226,257,287,318 en 348.
  • De resten bij deling door 7 zijn: 6,2,3,6,1,4,6,2,5,0,3 en 5. De redenering is analoog als hierboven

 6 januari 2023 is een vrijdag, dus zijn er in 2023 twee vrijdagen de dertiende, namelijk in januari en oktober: de dagnummers moeten modulo 7 gelijk zijn aan 6 en er komt in het rijtje dagnummers bij niet-schrikkeljaren inderdaad 2 keer een 6 voor.

Een telprobleem

Geplaatst op door

Op hoeveel manieren kan je een rijtje van 10 symbolen 0,1 of 2 maken zodat er nooit twee enen of twee twee na elkaar voorkomen?

Goed is dus 1200121001 en fout is 0012011202 omdat hier twee enen na elkaar voorkomen. 

Vorm de matrix

    \[A=\begin{pmatrix} 1&1&1\\1&0&1\\1&1&0\end{pmatrix}\]

Nummer de rijen en de kolommen met 0,1en 2

a_{00}=1 betekent: er is een mogelijkheid om na een 0 een tweede nul te plaatsen.
a_{11}=0 betekent : na een 1 kan er geen 1 komen.
a_{12}=1 betekent: na een 1 kan er een 2 komen.

Het is duidelijk dat de som van de elementen van deze matrix A het aantal goede tweetallen is: 00,01,02,10,12,20,21 . Er zijn 7 goede tweetallen.

Net zoals bij een directe wegenmatrix (soort overgangsmatrix) zal de som van de elementen van A^9 dan het aantal goede tientallen geven:

    \[A^9=\begin{pmatrix} 1393&985&985\\985&696&697\\985&697&696\end{pmatrix}\]

Het antwoord op de gestelde vraag is dan 8119.

Som van opeenvolgende getallen

Geplaatst op door

Op hoeveel manier kan je, bijvoorbeeld, 45 schrijven als som van opeenvolgende getallen? 

  • We stellen een formule op om de som van opeenvolgende getallen te berekenen. Stel n=m+(m+1)+\dots+(m+k-1). Hier bij is n de som, m het eerste getal en k het aantal getallen in die som.
  • Om die som te berekenen kan je de formule voor de som van de termen van een rekenkundige rij gebruiken: n=\dfrac{1}{2}k.(m+m+k-1).
  • Hieruit volgt:

        \[2n=k(2m+k-1)\]

  • Als k even is dan is 2m + k –  oneven en omgekeerd als k oneven is dan is 2m + k – 1 even. Bovendien is k kleiner dan 2m + k  – 1.
  • We moeten 2n dus schrijven als een product van een even getal en een oneven getal. De kleinste van die 2 factoren is k en dat is het aantal termen in de som.
  • Ontbinden we n in priemfactoren: n=2^r.p_1^{r_1}.\cdots .p_s^{r_s}. En dan is 2n=2^{r+1}.p_1^{r_1}.\cdots . p_s^{r_s}. Hierbij zijn p_i verschillende (oneven) priemgetallen. Dit moeten we dan schrijven als product van een oneven en even getal
  • Noteer S(n) het aantal mogelijkheden om n te schrijven als een som van opeenvolgende getallen, dan is het duidelijk dat

        \[S(n)=(r_1+1).\cdots.(r_s+1)-1\]

  • Terug naar ons voorbeeld n=45. dan is 2n=90=2.3^2.5^1 en is S(45)=(2+1)(1+1)-1=5. We kunnen 45 op 5 manieren schrijven als som van opeenvolgende getallen.
  • Hoe vinden we nu die sommen? We kunnen eerst m berekenen uit 2n=k(2m+k-1):  m=\dfrac{1}{2}(n-k+1) en we nemen k opeenvolgend als 2,3,5,6,9. Dit geeft:
  • \begin{array}{c|c|c} k&m&\text{som}\\ \hline 2&22&22+23\\3&14&14+15+16\\5&7&7+8+9+10+11\\6&5&5+6+7+8+9+10\\9&1&1+2+3+4+5+6+7+8+9\end{array}