Deze is gemaakt door Obi Andries , ook leerling van 4NAWE B van De Prins in Diest:
Bergparabool stijgt
keert terug naar de oorsprong
coördinaat nul
Categorie archieven: WisKunst
Nog enkele haiku’s
4NAWE B van de Prins Diest is zeer poëtisch aangelegd. Hier volgen nog drie haiku’s van respectievelijk Wout Koninckx, Fien Keirsmakers en Lou Marx:
Twee lijnen snijden
hoek geeft een stille waarheid
beperkt, maar geen eind
Driehoek en een lijn
delen door de helft precies
alles klopt altijd
Wortels van negen
waarschijnlijk denk je aan drie
vergeet niet min drie
Nieuwe haiku’s
Enkele leerlingen van 4NAWE B van de Prins in Diest hebben zich gewaagd aan een ‘wiskundige’ haiku. De eerste komt van Lars Nies en de tweede van Mathieu De Busser:
Waarheidstabel rolt
logische keuzes maken
leugen of waarheid
Berg of dal in beeld
tweedegraads is altijd leuk
x is er altijd
Haiku’s
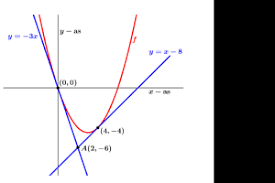
Tangenten kruisen
grafieken fluisteren zacht
wiskunde’s geheim
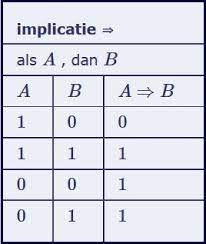
In de logica
redeneren als een kunst
wiskunde’s puzzel
Deze haiku’s zijn geschreven door Kato Appelen, leerling 6HUWE, de Prins Diest
Ook Chatgpt kan er iets van:
Rijen dansen strak
Fibonacci’s zachte cadans
Getal harmonie.
Formules in lucht
Grafieken als kunstwerken
Wiskunde’s poëzie.
Geometrie zingt
Driehoeken en cirkel
Ruimte in getal.
Algebra’s taal
Onbekenden ontvouwen
Wiskunde onthult.
Calculus stroomt voort
Limieten, derivaten
Wiskundig eb en vloed.
Nog haiku’s
de les wiskunde
met veel ongelijnd papier
altijd een plezier
ingezonden door Kiary Claessens, leerling 6 HUM , de Prins Diest
Exponent vol zwier
krachten stijgend als een vlam
wiskunde’s vuurzee
ingezonden door Maité Vanluyten, leerling 6 HUM, de Prins Diest