In dit artikel bespreken we problemen waarin men beschikt over 2 lege kannen, zonder maatstreepjes. Verder is er een kraan waarmee men de kannen kan vullen en een gootsteen waarin men de kannen kan leeggieten. We aanvaarden volgende handelingen : Een kan volledig leeggieten, een kan helemaal vullen met de kraan, water van de ene kan overhevelen in de andere kan totdat de ene helemaal leeg is of de andere helemaal vol. Je vindt ook een Python programma om het probleem op te lossen
Categorie archieven: Artikels
Gemiddelden visueel voorgesteld
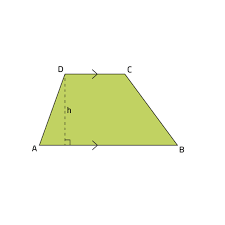 Lees in dit artikel hoe je in een trapezium het rekenkundig, het meetkundig, het harmonisch en het kwadratisch gemiddelde kan terugvinden.
Lees in dit artikel hoe je in een trapezium het rekenkundig, het meetkundig, het harmonisch en het kwadratisch gemiddelde kan terugvinden.
Derdegraads vergelijkingen: vervolg.
In een vorig artikel hebben we de formules van Cardano besproken voor het oplossen van een willekeurige vergelijking van graad 3. Maar wat heeft de symmetrische groep van orde 6,![]() hier mee te maken? En wat is de discriminant van zo een vergelijking? Is dat dan een veralgemening van de discriminant van een vergelijking van graad 2? Wil je hierover meer weten , lees dat dit vervolgartikel.
hier mee te maken? En wat is de discriminant van zo een vergelijking? Is dat dan een veralgemening van de discriminant van een vergelijking van graad 2? Wil je hierover meer weten , lees dat dit vervolgartikel.
Derdegraads vergelijkingen
Een algemene tweedegraads vergelijking ![]() kan worden opgelost met de formule
kan worden opgelost met de formule
![]()
We vragen ons af of er voor een willekeurige derdegraads vergelijking ![]() , met
, met ![]() , ook een algemene oplossingsmethode bestaat. We weten wel al zeker dat elke derdegraads vergelijking minstens 1 re\”ele oplossing heeft. Dit in tegenstelling tot de tweedegraads vergelijkingen waar niet elke vergelijking een re\”ele oplossing heeft.
, ook een algemene oplossingsmethode bestaat. We weten wel al zeker dat elke derdegraads vergelijking minstens 1 re\”ele oplossing heeft. Dit in tegenstelling tot de tweedegraads vergelijkingen waar niet elke vergelijking een re\”ele oplossing heeft.
Lees hier verder.
Overdekkingen van het vlak
We gaan op zoek naar regelmatige bedekkingen van het vlak: dit zijn bedekkingen met regelmatige n-hoeken met alle dezelfde lengte als zijde. Het vlak is dan de unie van al die veelhoeken en de doorsnede van twee veelhoeken is ledig, ofwel een punt ofwel een zijde. We eisen ook dat de hoekpunten gelijkwaardig zijn, dus dat in een punt steeds dezelfde veelhoeken in dezelfde aantallen en in dezelfde volgorde voorkomen. Noteren we met ![]() het aantal verschillende veelhoeken in een bepaald knooppunt.
het aantal verschillende veelhoeken in een bepaald knooppunt.
De waarde van een hoek van een regelmatige n-hoek is
![]()
Neem eerst het geval ![]() . Noteer met m het aantal veelhoeken in een knooppunt. Dan moet
. Noteer met m het aantal veelhoeken in een knooppunt. Dan moet ![]() . Hieruit volgt dat
. Hieruit volgt dat ![]() of
of ![]() . Hierbij zijn uiteraard m en n natuurlijke getallen. De enige oplossingen zijn:
. Hierbij zijn uiteraard m en n natuurlijke getallen. De enige oplossingen zijn:
![]()
Neem nu ![]() ( we spreken dan van Archimedische vlakvullingen) en stel dat er a regelmatige m-hoeken en b regelmatige n-hoeken samenkomen, dan moet
( we spreken dan van Archimedische vlakvullingen) en stel dat er a regelmatige m-hoeken en b regelmatige n-hoeken samenkomen, dan moet ![]() of
of
![]()
![]()
Geval 1: ![]() en
en ![]() , dan is
, dan is ![]() en zijn de enige natuurlijke oplossingen:
en zijn de enige natuurlijke oplossingen: ![]() en
en ![]() . De oplossing
. De oplossing ![]() hebben we al en
hebben we al en ![]() geeft geen regelmatige overdekking. De twee oplossingen geven we volgende typering:
geeft geen regelmatige overdekking. De twee oplossingen geven we volgende typering: ![]() ( 1 driehoek en 2 twaalfhoeken) en
( 1 driehoek en 2 twaalfhoeken) en ![]() (1 vierkant en 2 achthoeken).
(1 vierkant en 2 achthoeken).

Geval 2: ![]() en
en ![]() , dan is
, dan is ![]() en is de enige natuurlijke oplossing:
en is de enige natuurlijke oplossing: ![]() en die hebben we al gehad bij
en die hebben we al gehad bij ![]() .
.
Geval 3: ![]() en
en ![]() , dan is
, dan is ![]() en zijn de enige natuurlijke oplossingen:
en zijn de enige natuurlijke oplossingen: ![]() . Typering:
. Typering: ![]() ( een zeshoek en 4 driehoeken)
( een zeshoek en 4 driehoeken) Geval 4:
Geval 4: ![]() en
en ![]() , dan is
, dan is ![]() en zijn de enige natuurlijke oplossingen:
en zijn de enige natuurlijke oplossingen: ![]() ,
, ![]() en
en ![]() . De oplossing
. De oplossing ![]() hebben we al. Bovendien geven
hebben we al. Bovendien geven ![]() en
en ![]() dezelfde oplossing.Rest nog het geval
dezelfde oplossing.Rest nog het geval ![]() (2 zeshoeken en 2 driehoeken).
(2 zeshoeken en 2 driehoeken). 
Geval 5: ![]() en
en ![]() , dan is
, dan is ![]() en is de enige natuurlijke oplossing:
en is de enige natuurlijke oplossing: ![]() . Type
. Type ![]() ( twee vierkanten en drie driehoeken). We verfijnen de typering: links de overdekking
( twee vierkanten en drie driehoeken). We verfijnen de typering: links de overdekking ![]() en rechts
en rechts ![]() .
.
Neem nu ![]() en stel dat er a regelmatige m-hoeken, b regelmatige n-hoeken en c regelmatige p-hoeken samenkomen, dan moet
en stel dat er a regelmatige m-hoeken, b regelmatige n-hoeken en c regelmatige p-hoeken samenkomen, dan moet ![]() of
of
![]()
Geval 1: ![]() . Dan is
. Dan is ![]() . Onderzoek van verschillende mogelijkheden geeft
. Onderzoek van verschillende mogelijkheden geeft ![]() . Enkel
. Enkel ![]() levert een nieuwe bestaande overdekking. We krijgen een zeshoek, een twaalfhoek en een vierkant in elk knooppunt.
levert een nieuwe bestaande overdekking. We krijgen een zeshoek, een twaalfhoek en een vierkant in elk knooppunt. 
Geval 2: ![]() . Enkel
. Enkel ![]() levert een nieuwe bestaande overdekking. We krijgen twee vierkanten , een zeshoek en een driehoek in elk knooppunt.
levert een nieuwe bestaande overdekking. We krijgen twee vierkanten , een zeshoek en een driehoek in elk knooppunt. 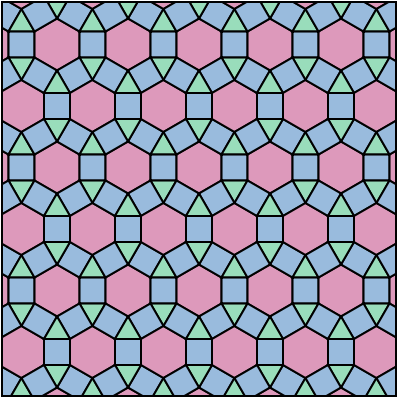 Geval 3:
Geval 3: ![]() . Deze combinatie levert geen nieuwe oplossingen.
. Deze combinatie levert geen nieuwe oplossingen.
Geval 4: ![]() . Deze combinatie levert geen nieuwe oplossingen.
. Deze combinatie levert geen nieuwe oplossingen.
Situaties met ![]() of
of ![]() kunnen niet voorkomen want
kunnen niet voorkomen want ![]() .
.