Categorie archieven: Meetkunde

Verdubbelingsformule

Geplaatst op door

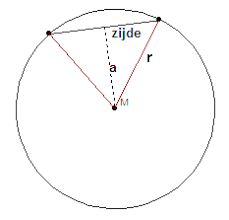
De lengte x  van een koorde, die een boog onderspant, gelijk aan de helft van de boog, die bij een gegeven koorde a hoort, is

    \[x=\sqrt{2r^2-r\sqrt{4r^2-a^2}}\]

Hierbij is r de straal van de cirkel.

Als a de zijden van een regelmatige n-hoek is, dan is x de zijden van een regelmatige 2n-hoek. Zo kunnen we bijvoorbeeld de zijde van een regelmatige twaalfhoek berekenen. De zijde van een regelmatige zeshoek is gelijk aan de straal r van de omgeschreven cirkel, en dus is

    \[z_{12}=\sqrt{2-\sqrt{3}}r\]

We kunnen uit de formule ook a berekenen in functie van x en dan vinden we

    \[a=\frac{x\sqrt{4r^2-x^2}}{r}\]

Uit de zijde van een regelmatige zeshoek kunnen we zo de zijden van een gelijkzijdige driehoek berekenen:

    \[z_6=\sqrt{3}r\]

Koordenvierhoek

Geplaatst op door

 

Een koordenvierhoek is een vierhoek waarvan de hoekpunten op een cirkel gelegen zijn. Deze cirkel noemen we dan de omgeschreven cirkel.

Een paar eigenschappen:

  • Bij een koordenvierhoek zijn de overstaande hoeken supplementair en omgekeerd, als bij een vierhoek elke twee overstaande hoeken supplementair zijn, dan is die vierhoek een koordenvierhoek. Bijgevolg zijn een vierkant , een rechthoek , een gelijkbenig trapezium  allemaal koordenvierhoeken.
  • Van een koordenvierhoek is het product van de diagonalen gelijk aan de som van de producten van de overstaande zijden  en omgekeerd (stelling van Ptolemeus): 
           

        \[AC.BD=AB.CD+AD.BC\]

  • De verhouding van de diagonalen van een koordenvierhoek is gelijk aan de verhouding van de sommen van de producten van de zijden, die in hun uiteinden samenkomen:

        \[\frac{AC}{BD}=\frac{AB.AD+CD.BC}{AB. BC+AD.CD}\]