OEIS

Geplaatst op 4 juni 2025 door admin

In de wereld van wiskunde en informatica is er een schat aan patronen en rijen die ons omringen. Deze worden niet alleen bestudeerd voor hun intrinsieke schoonheid, maar ook voor hun praktische toepassingen in verschillende wetenschappelijke en technologische disciplines. Een van de meest waardevolle bronnen voor het ontdekken en begrijpen van deze rijen is de Online Encyclopedia of Integer Sequences (OEIS).

De OEIS, opgericht in 1964 door Neil Sloane( een Amerikaans wiskundige van Britse afkomst), is een uitgebreide online database van meer dan 350.000 rijen gehele getallen. Elke rij is zorgvuldig gedocumenteerd met zijn beginwaarden, een beschrijving van het patroon, mogelijke wiskundige verklaringen en vaak voorkomende toepassingen. Wat begon als een persoonlijk project van Sloane, is uitgegroeid tot een onschatbare bron voor wiskundigen, informatici en liefhebbers van getallenreeksen wereldwijd. De eerste versie van OEIS stond op ponskaarten. De volgende verscheen in 1973 als boek met de titel A handboek of integer Sequences, met 2400 rijen. De editie van 1995 telde er 5487. De internet versie volgde in 1996 en sindsdien komen er jaarlijks ongeveer 10000 rijen bij.

Enkele rijen uit de OEIS:

Fibonacci-rij (A000045):
$0, 1, 1, 2, 3, 5, 8, 13, 21, 34, \dots$
De Fibonacci-reeksijtwee voorgaande getallen. Deze reeks vindt toepassingen in natuurlijke fenomenen, zoals de rangschikking van bloemblaadjes in bloemen en de groei van populaties.
Priemgetallen (A000040):
$2, 3, 5, 7, 11, 13, 17, 19, 23, 29, \dots$
De rij van priemgetallen bevat getallen die alleen deelbaar zijn door 1 en zichzelf. Ze vormen de bouwstenen van moderne cryptografie en hebben diepgaande implicaties voor de informatieveiligheid.
De rij van de gelukkige getallen (A0077700)

Een gelukkig getal is een getal waarbij, als je de som van de kwadraten van zijn cijfers herhaaldelijk neemt, je uiteindelijk op 1 uitkomt. Bijvoorbeeld:
- 19 → 1² + 9² = 82
- 8² + 2² = 68
- 6² + 8² = 100
- 1² + 0² + 0² = 1
Ze worden “gelukkig” genoemd omdat ze eindigen in 1 in plaats van in een eindeloze cyclus. Deze reeks heeft een verrassende aantrekkingskracht en is ook populair bij programmeeroefeningen.
$1, 11, 21, 1211, 111221, 312211, \dots$
Een verbazingwekkend patroon: je beschrijft het vorige getal.
- “1” wordt “één 1” → 11
- “11” wordt “twee 1-en” → 21
- “21” wordt “één 2, één 1” → 1211, enzovoort.
Deze rij groeit snel en werd populair gemaakt door John Conway, die ook interessante eigenschappen aantoonde, zoals het feit dat alle getallen asymptotisch vervallen in “atomen” — vaste bouwstenen.
$1, 7, 19, 37, 61, 91, 127, \dots$
Dit zijn getallen die je krijgt als je punten neerzet in de vorm van een hexagonale rasterstructuur met concentrische ringen eromheen. Ze komen voor in wiskundige kunst, kristallografie en zelfs in bordspellen zoals Settlers of Catan!

Bezoek oeis.org en probeer zelf een rij zoals 3, 6, 12, 24, 48... in te voeren. Grote kans dat je ontdekt welk patroon daarachter zit — of dat iemand anders het al eerder heeft gezien, onderzocht en vastgelegd. Een deel van het antwoord vind je hieronder.

Inverse en complementaire rijen

Geplaatst op 27 december 2020 door admin

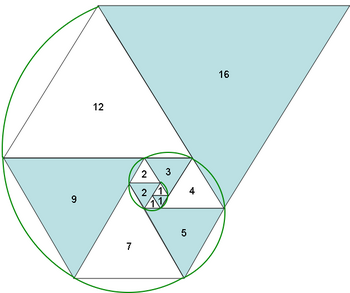
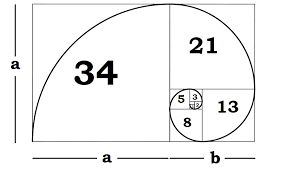
Gegeven is een rij f(n) met $n=0,1,2,...$ . Definieer dan

$g(n)=k \text{ als } f(k)<n\leq f(k+1)$

Een voorbeeld: f(n)=0,0,0,1,2,3,3,4,5,6,7,10,… dan is g(n)=3,4,5,7,8,9,10,11,11,11

g(n) is eigenlijk het aantal termen in de rij f(n) die kleiner zijn dan n.
Als we op g(n) dezelfde procedure toepassen als op f(n), dan bekomen we terug f(n). Vandaar dat we g(n) de inverse rij van f(n) noemen.

Construeer nu volgende twee rijen: $F(n)=f(n)+n$ en $G(n)=g(n)+n$ . In ons voorbeeld is $F(n)=1,2,3,5,7,9,10,12,14,...$ en $G(n)=4,6,8,11,13,15,17,19,20,...$ . Wat stellen we nu vast? De twee rijen F(n) en G(n) bevatten samen juist 1 keer elk positief natuurlijk getal. Dit feit en het omgekeerde werden ontdekt en bewezen in 1954 door de wiskundigen Lambek (zie hieronder) en Moser,onder de voorwaarden dat(n)eng(n)niet-dalenderijen zijn van natuurlijke getallen.

De rijen F(n) en G(n) noemen we complementaire rijen.

Als het expliciet voorschrift van een rij gekend is, kunnen we deze stelling gebruiken om het voorschrift te bepalen van de complementaire rij. Zo kunnen we de natuurlijke getallen bijvoorbeeld opsplitsen in 2 rijen F(n) van de kwadraten en G(n) van de niet kwadraten: $F(n)=1,4,9,16,25,...$ en $G(n)=2,3,5,6,7,8,10,...$ . We weten dat $F(n)=n^2$ . Wat is nu het voorschrift van G(n)?

F(n) en G(n) zijn complementair en dus zijn $f(n)=F(n)-n=0,2,6,12,20,...$ en $g(n)=G(n)-n=1,1,2,2,2,2,3,...$ elkaars inverse. Nu is $f(n-=n^2-n$ . Dan is $g(n)=k$ als en slechts als $f(k)<n\leq f(k+1)$ of m.a.w. $k^2-k<n\leq k^2+k$ . Omdat n en k een natuurlijke getallen zijn is dan ook $k^2-k+\frac{1}{4}<n< k^2+k\frac{1}{4}$ . Hieruit volgt dan uiteindelijk dat $\sqrt{n}-\frac{1}{2}<k<\sqrt{n}+\frac{1}{2}$ . Dus : $g(n)=\lfloor \sqrt{n}+\frac{1}{2} \rfloor$ en

$G(n)=n+\lfloor \sqrt{n}+\frac{1}{2} \rfloor$

De rij van Padovan en het plastisch getal

Geplaatst op 10 november 2019 door admin

Gelijkaardig aan de rij van Fibonacci, kunnen we ook de rij van Padovan definiëren, als de rij met $p_1=p_2=1$ en

$p_n=p_{n-2}+p_{n-3}$

De rij van Padovan is vernoemd naar de schrijver en architect Richard Padovan die zijn ontdekking toegeschreef aan de Nederlandse architect Hans van der Laan . Hieronder zie je een spiraal van gelijkzijdige driehoeken waarvan de lengten der zijden gelijk zijn aan de de getallen uit de rij van Padovan.

Als we de rij bestuderen van de quotiënten van twee opeenvolgende getallen uit de rij van Padovan, bekomen we volgende rij : $2,1,\frac{3}{2},\frac{4}{3},\frac{5}{4},\frac{7}{5},\frac{9}{7},...$ . We vermoeden dat deze rij convergeert naar een limiet L.
$a_n=\frac{p_n}{p_{n-1}}=\frac{p_{n-2}}{p_{n-1}}+\frac{p_{n-3}}{p_{n-1}}=\frac{p_{n-2}}{p_{n-1}}+\frac{p_{n-3}}{p_{n-2}}\frac{p_{n-2}}{p_{n-1}}$ . Dus is $a_n=\frac{1}{a_{n-1}}+\frac{1}{a_{n-2}}\frac{1}{a_{n-1}}$ . In de limiet wordt dit $L=\frac{1}{L}+\frac{1}{L^2}$ . Bijgevolg voldoet de limiet L aan de betrekking

$L^3-L-1=0$

Zo vinden we voor L de benaderende waarde $1,3247$ .

Dit getal noemen we het plastisch getal. Het plastisch getal heeft met de gulden snede nog meer eigenschappen gemeen, maar sommigen gaan nog verder en dichten aan deze getallen verregaande eigenschappen toe omtrent schoonheid.

Fibonacci en de gulden snede

Geplaatst op 26 oktober 2019 door admin

De rij van Fibonacci: 1,1,2,3,5,8,13,21,… wordt gevormd door met twee enen te beginnen en dan is elke term de som van de vorige twee termen, dus:

$a_1=a_2=1 \text{ en } a_{n+2}=a_{n+1}+a_n$

Vorm nu de rij $s_n$ door twee opeenvolgende termen van de rij van Fibonacci te delen door elkaar:

$s_n=\frac{a_{n+1}}{a_n}$

Een paar termen van die rij zijn : $1,2,\frac{3}{2},\frac{5}{3},\frac{8}{5},...$ . Wat zou de limiet van deze rij nu zijn?

We vermoeden dat deze limiet bestaat. Noteer de limiet met L.
Nu geldt $s_n=\frac{a_{n+1}}{a_n}=\frac{a_n+a_{n-1}}{a_n}=1+\frac{1}{s_{n-1}}$ . Dus voldoet de limiet L aan de betrekking $L=1+\frac{1}{L}$ . Dit geeft de vergelijking

$L^2-L-1=0$

De positieve oplossing van deze vergelijking is $\frac{1+\sqrt{5}}{2}=\varphi=1,6180 3398 8749 8948 482...$ , de gulden snede!

Lineaire recursieve rijen

Geplaatst op 16 maart 2018 door admin

Een rij $a_n$ voldoet aan een lineaire recurrentie als

$c_ka_{n+k}+c_{k-1}a_{n-k-1}+\cdots+c_1a_{n+1}+c_0a_n=0$

De rij $a_n$ noemt men dan een lineaire recursieve rij.
De karakteristieke veelterm van bovenstaande lineaire recurrentie is de veelterm

$f(x)=c_kx^k+c_{k-1}x^{k-1}+\cdots c_1x+c_0$

Als we $f(x)$ in $\mathbb{C}$ kunnen ontbinden als

$c_k(x-r_1)^{m_1}(x-r_2)^{m_2}\cdotsc_k(x-r_l)^{m_l}$

dan voldoet $a_n$ aan de lineaire recurrentie als en slechts als er functies $g_i(x)$ , met graad kleiner of gelijk aan $m_i-1$ , bestaan zodat

$a_n=g_1(n)r_1^n+\cdots+g_l(n)r_l^n$

Als $m_1=m_2=\cdots=m_l=1$ , dan zijn alle functies $g_i(x)$ constanten.

Enkele speciale gevallen:

Bij een rekenkundige rij is $a_{n+1}=a_n+v$ met $a_0=a$ . Dit is geen lineaire recurrentie. Maar nu is ook $a_{n+2}=a_{n+1}+v$ . Aftrekken van de twee formules geeft : $a_{n+2}-2a_{n+1}+a_n=0$ . Dits is wel een lineaire recurrentie met karakteristieke veelterm $x^2-2x+1=(x-1)^2$ . Bijgevolg is $a_n=(An+B).1^n$ . Het is duidelijk dat $B=a$ , de beginterm van de rij en $A=v$ , het verschil van de rij. Zodoende is het algemeen voorschrift $a_n=n.v+a$ voor $n=0,1,...$
Bij een meetkundige rij is $a_{n+1}=a_n.q$ met $a_0=a$ . Dit is een lineaire recurrentie met karakteristieke veelterm $x-q$ . Bijgevolg is $a_n=A.q^n$ . Uit $a_0=a$ volgt dat $A=a$ en dus is het algemeen voorschrift $a_n=a.q^n$ voor $n=0,1,...$

Voorbeeld : $a_0=1$ en $a_1=4$ en elke ander term is het rekenkundig gemiddelde van de twee vorige termen. Een aantal termen van de rij: $1,4,\frac{5}{2},\frac{13}{4},...$ . Om de algemene term van de rij te bepalen, zoeken we eerst de karakteristieke veelterm van de lineaire recurrentie: $2a_{n+2}-a_{n+1}-a_n=0$ . Dan is $f(x)=2x^2-x-1=2(x-1)(x+\frac{1}{2}$ . Bijgevolg is $a_n=A1^n+B\Big(-\frac{1}{2}\Big)^n=A+B\Big(-\frac{1}{2}\Big)^n$ . Om A en B te bepalen gebruiken we dat $a_0=1$ en $a_1=4$ . Hieruit volgt dat $A=3$ en $B=-2$ , zodat $a_n=3-2\Big(-\frac{1}{2}\Big)^n$

Wiskunde is leuk

Categorie archieven: Rijen en reeksen

OEIS

Inverse en complementaire rijen

De rij van Padovan en het plastisch getal

Fibonacci en de gulden snede

Lineaire recursieve rijen