Schrijf een Python programma dat alle natuurlijke delers van een gegeven geheel getal berekent.
We definiëren eerst een functie die onderzoekt welke getallen een deler zijn en dan die getallen opslaat in een lijst.
Categorie archieven: Python
Kleinste getal in een rij zoeken;
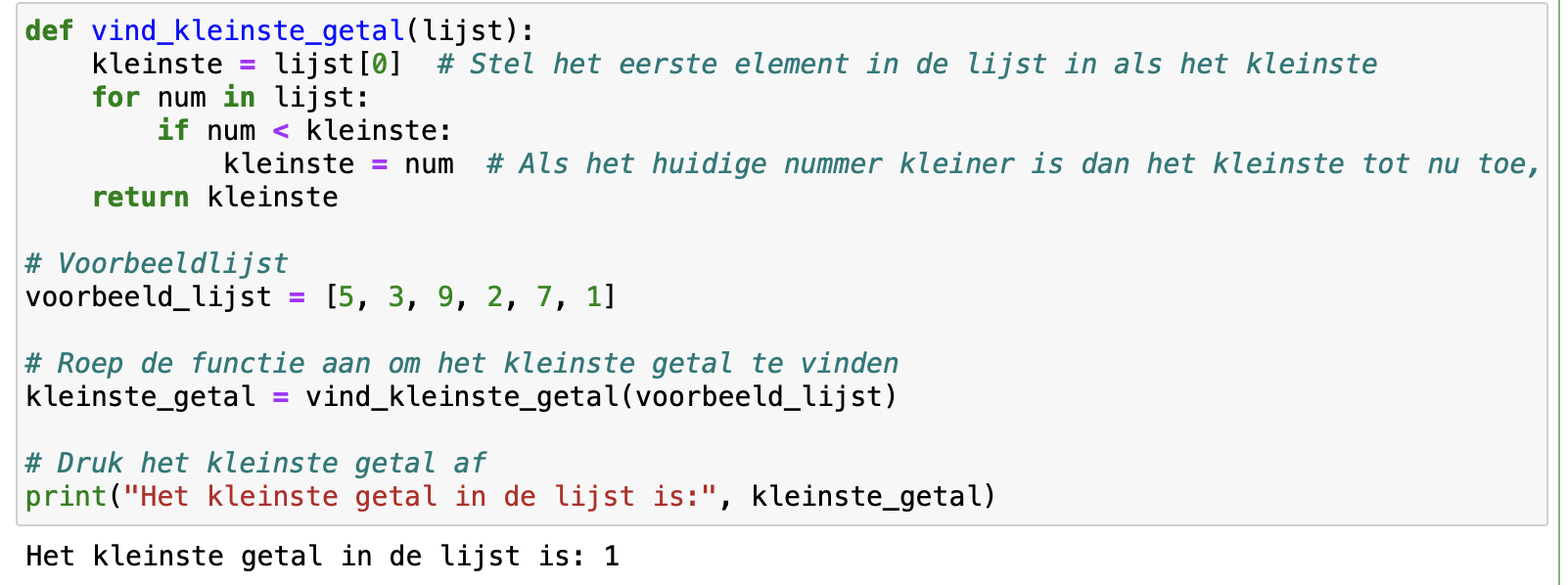
Een Python programma om het kleinste getal in een lijst terug te vinden:
Grootste gemene deler en kleinste gemene veelvoud
Een programma in Python om de god en het ktv van twee getallen te berekenen. We maken gebruik van het algoritme van Euclides, dat zegt dat de grootste gemene deler van a en b ( met a>b) gelijk is aan de grootste gemene deler van b en de rest bij deling van a door b. Verder gebruiken we de formule dat het product van de ggd en het kgv gelijk is aan het product van de twee gegeven getallen.
een voorbeeld:
Een probleem uit getallenleer
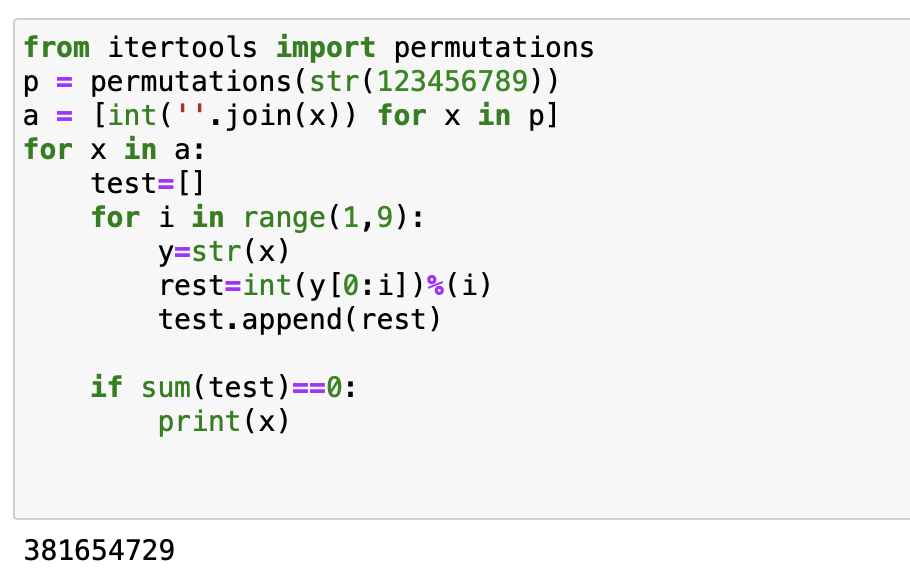
Een natuurlijk getal bestaat uit 9 verschillende cijfers 1 tot en met 9. Schrijft men het opnieuw met telkens de eerste k cijfers, dan is het getal een veelvoud van k. Om welk getal gaat het?
- Het getal gevormd door de eerste 2 cijfers is dus deelbaar door 2, gevormd door de eerste 3 cijfers door 3,…Het getal zelf is dus deelbaar door 9.
- Dat laatste is altijd voldaan omdat de som der cijfers gelijk is aan 45 en dat is deelbaar door 9. Bijgevolg is het getal zelf ook deelbaar door 9.
- We moeten dus enkel controleren voor de eerste 2 tot de eerste 8 cijfers.
- Het volgende programma in Python geeft de oplossing:
Python: de zeef van Eratosthenes
De zeef van Eratosthenes (Bibliothecaris van de bibliotheek van Alexandrië rond 240 v.C.) is een algoritme om priemgetallen te bepalen kleiner dan een gegeven getal n:
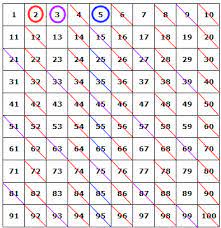
- Maak een geordende lijst van alle getallen van 2 tot n.
- Neem het kleinste getal in deze lijst en schrap alle veelvouden van dit getal ( het getal zelf niet!).
- Neem het volgende getal in de lijst en doe hiervoor hetzelfde.
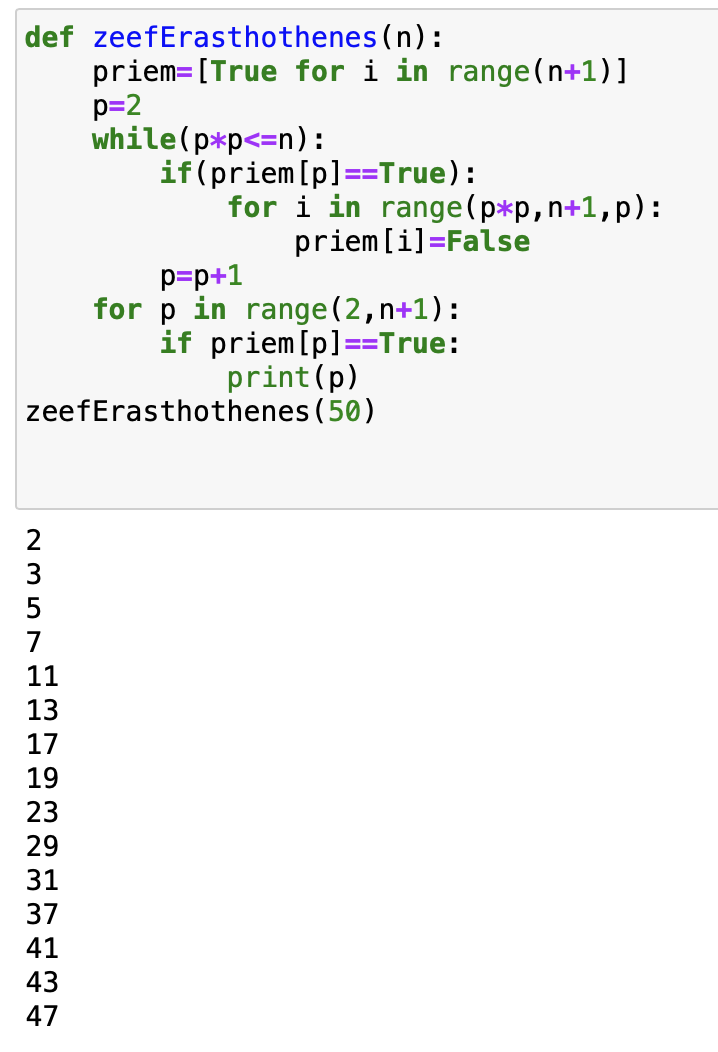
Een programma in Python geeft bijvoorbeeld alle priemgetallen kleiner dan 50
:
Uitleg:
- Neem een lijst van lengte n en zet op elke plaats de boolse waarde True.
- Begin met p=2 en zet alle veelvouden van 2 in de lijst op False. Begin met het eerste veelvoud van 2 na 2 zelf: dat is 2*2.
- Neem dan p=3 en zet alle veelvouden van 3 op False, beginnend met 3*3
(want alle vroegere veelvouden zijn sowieso al op False gezet. - Doe zo verder zolang p*p kleiner is dan de gegeven waarde n.