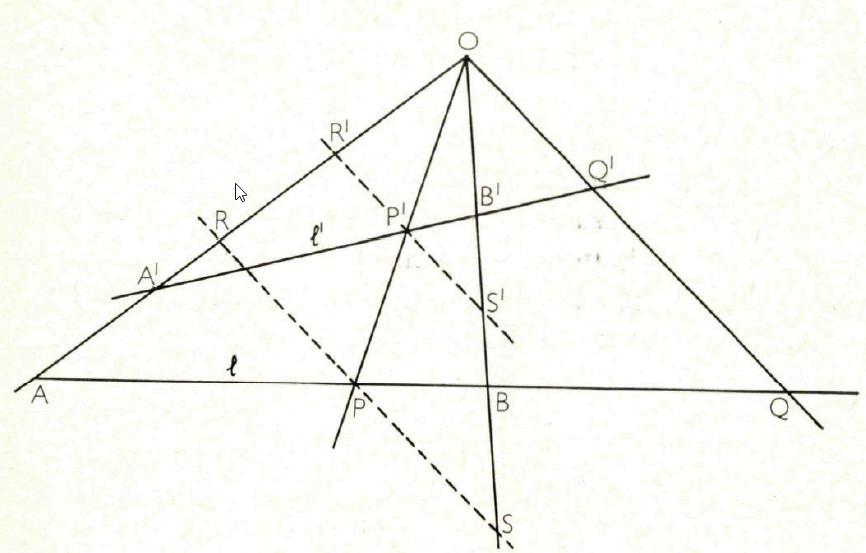
We weten dat de binnen- en buiten bissectrice van de hoek O in driehoek OAB  de overstaande zijde verdeelt in een harmonisch puntenviertal ABPQ. Als we een andere snijlijn nemen met de 4 rechten die uit O vertrekken en hun snijpunten noteren met A’,B’,P’ en Q’, dan is ook dit een harmonisch puntenviertal, omdat ook in de driehoek OA’B’ de bissectrice stelling geldt. We noemen de vier rechten uit C een harmonische vierstraal.

Maar we hebben de bissectrices niet nodig. We kunnen algemeen een harmonische vierstraal definieren als een geordend viertal concurrente rechten waarbij de snijpunten met een willekeurige transversaal een harmonisch puntenviertal opleveren.

Dit is een goede definitie want stel dat in bovenstaande tekening , dan zal , voor de willekeurige snijlijn l’, ook . Construeer door P en P’ rechten evenwijdig met OQ. Uit de gelijkvormigheid van driehoeken APR en AQO volgt dat . Uit de gelijkvormigheid van driehoeken PBS en QBO volgt dat . Uit het harmonisch zijn volgt dat de rechterleden in deze betrekkingen tegengesteld zijn, dus moet ook . Maar dan is ook . Uit de gelijkvormigheid van driehoeken A’P’R’ en A’Q’O enerzijds en driehoeken P’B’S’ en Q’B’O anderzijds volgt dan dat .