Als p,q en r priemgetallen zijn groter dan 3, bewijs dan dat ![]() geen priemgetal is.
geen priemgetal is.
Antwoord
- Elk priemgetal x is van de vorm
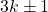 .
. - Dan is
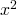 van de vorm
van de vorm 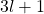 .
. - De som van 3 priemgetallen is dan :
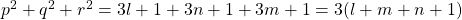 .
. - Dus is
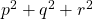 niet priem.
niet priem.
Als ![]() een priemgetal is, dan is k een macht van 2. Bewijs.
een priemgetal is, dan is k een macht van 2. Bewijs.
Antwoord
- Stel dat k geen macht van 2 is, dan is
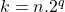 , waarbij n zeker oneven is.
, waarbij n zeker oneven is. - Nu is
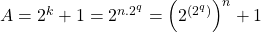 .
. - Algemeen geldt er dat , bij oneven n,
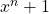 steeds deelbaar is door
steeds deelbaar is door 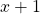 .
. - Bijgevolg is A deelbaar door
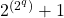 en hebben we een tegenspraak.
en hebben we een tegenspraak. - Dus is k wel een macht van 2.
