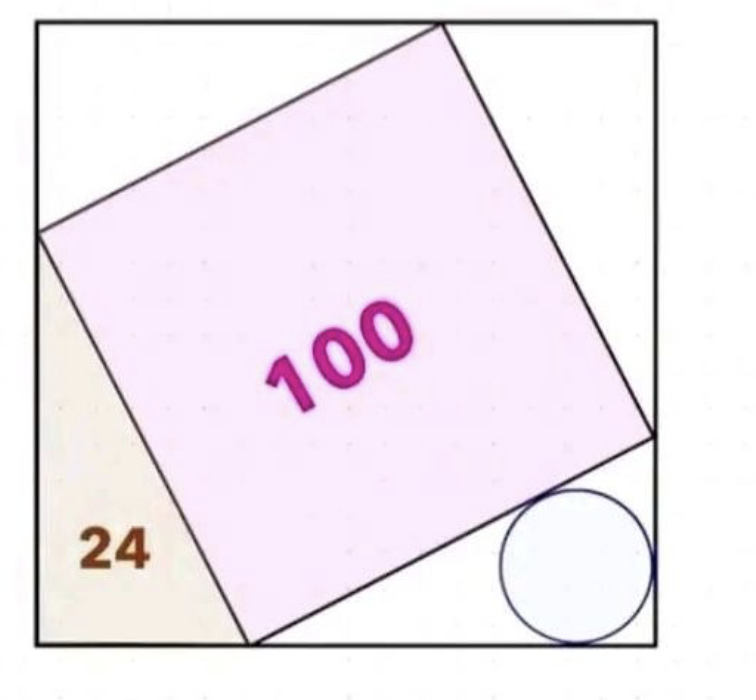
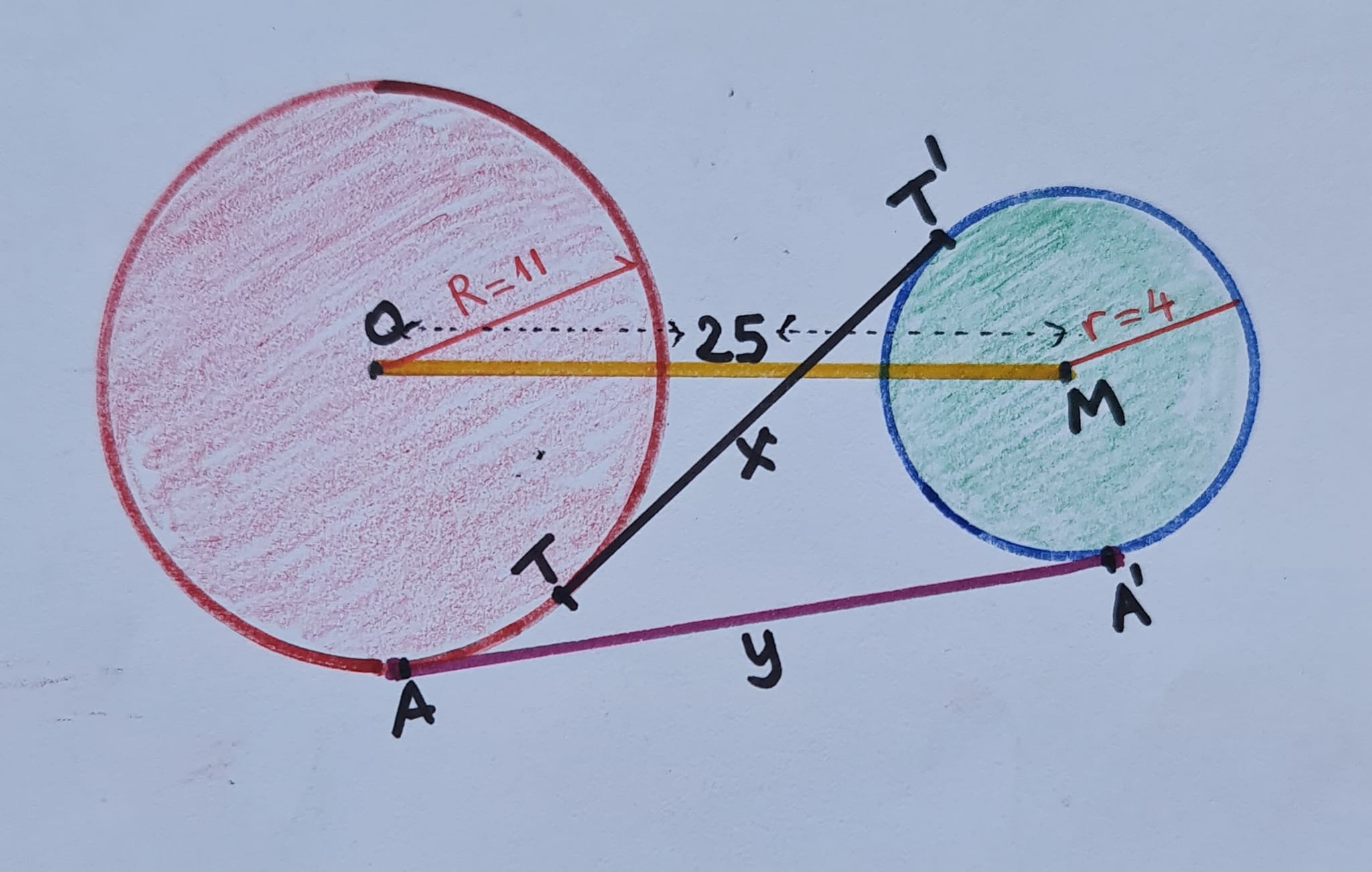
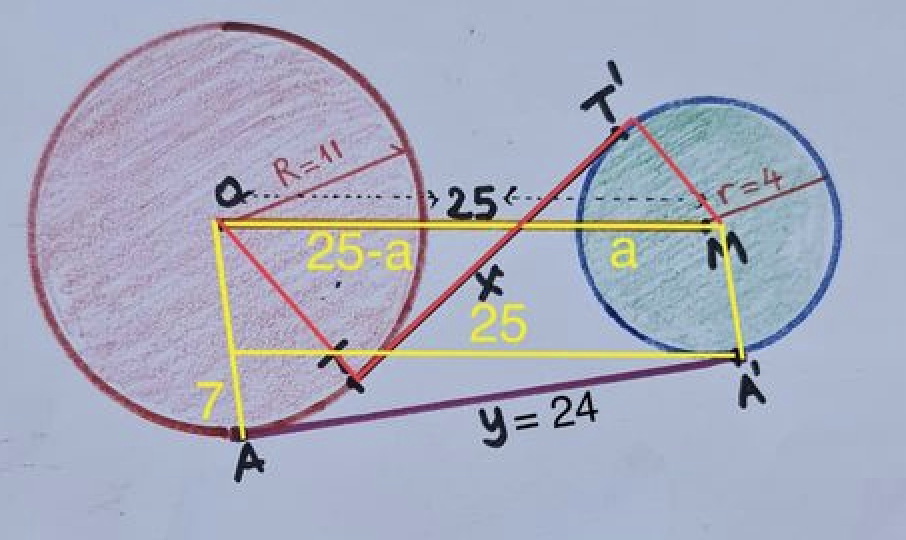
Bereken
![]()
Antwoord
- Een mogelijkheid is om het binomium van Newton te gebruiken. Gaan we niet doen…
- Stel
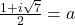 en
en 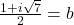 .
. - Dan is
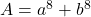 .
. - Nu is het duidelijk dat
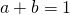 en
en 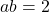 .
. - We weten dat
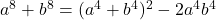 . Analoog is
. Analoog is 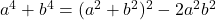 en evenzo is
en evenzo is 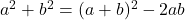 .
. - De laatste betrekking leert ons dat
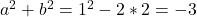 .
. - Dan is
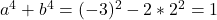 .
. - Tenslotte is
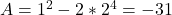 .
.