Voor heel wat praktische problemen moet men een bepaalde integraal ![]() oplossen. De meest wiskundige manier is op zoek gaan naar een primitieve functie F(x) van f(x) en dan is
oplossen. De meest wiskundige manier is op zoek gaan naar een primitieve functie F(x) van f(x) en dan is ![]() . Maar soms is het berekenen van een primitieve functie een zeer lastige of onmogelijke taak. Is het in die gevallen dan onmogelijk om de bepaalde integraal te berekenen?
. Maar soms is het berekenen van een primitieve functie een zeer lastige of onmogelijke taak. Is het in die gevallen dan onmogelijk om de bepaalde integraal te berekenen?
Thomas Simpson heeft een regel neergeschreven om ![]() te benaderen:
te benaderen:
- Verdeel
![Rendered by QuickLaTeX.com [a,b]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-611c86eb16b0fb9954e2532a2f68b269_l3.png) in een even ,n , aantal stukken en stel
in een even ,n , aantal stukken en stel 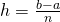 .
. - Bereken de functie waarden
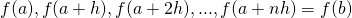 .
. - Nu is
![Rendered by QuickLaTeX.com \int_a^b f(x)\ dx \approx \frac{h}{3}\Big [ f(a)+f(b)+4\Big(f(a+h)+f(a+3h)+\cdots+f(a+(n-1)h\Big)+2\Big(f(a+2h)+f(a+4h)+\cdots+f(a+(n-2)h)\Big)\Big]](http://www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-f59df2699267624b400f73f5e7ba56e1_l3.png)
Simson bekwam zijn formule door de bepaalde integraal te interpreteren als een oppervlakte en het gebied onder de grafiek van ![]() over
over ![]() te benaderen door de oppervlakte onder een parabool door de punten
te benaderen door de oppervlakte onder een parabool door de punten ![]() ,
,![]() en
en ![]() .
.
Voorbeeld: Bereken ![]()
Neem ![]() , dan us
, dan us ![]() en kunnen we de bepaalde integraal benaderen door
en kunnen we de bepaalde integraal benaderen door ![]()


