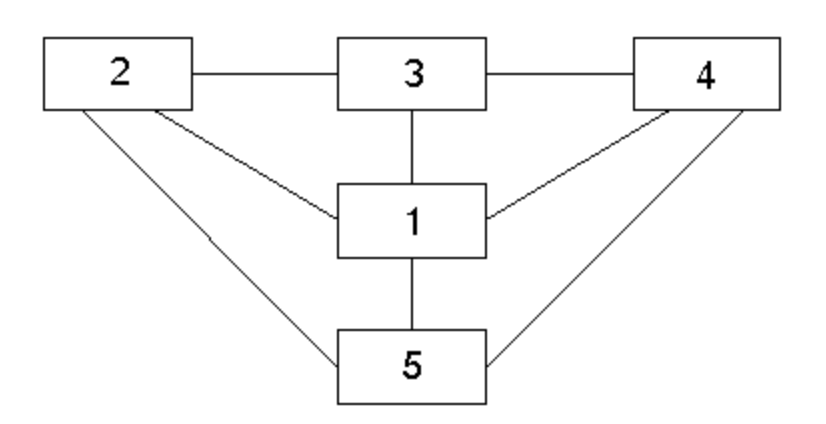
Kansen en matrices | Wiskunde is leuk

Een cavia bevindt zich in kamer 2. Ze kan deze kamer verlaten naar kamer 3,1 of 5 en dit met even grote waarschijnlijkheid. Hoe groot is de kans dat de cavia zich na 4 verplaatsingen in kamer 5 bevindt?

Noteer met a,b,c,d,e de kans dat de cavia zich op een zeker moment in kamer 1,2,3,4,5 bevindt. Met $a_i,b_i,c_i,d_i,e_i$ noteren we de kans dat het beestje zich, na i verplaatsingen, in kamer 1,2,3,4,5 bevindt.

Dan is bijvoorbeeld $a_1=0*a+\frac{1}{3}*b+\frac{1}{3}*c+\frac{1}{3}*d+\frac{1}{3}*e$ . We kunnen voor $b_1,c_1,d_1,e_1$ gelijkaardige formules vinden. Het is makkelijker die gegevens in een matrix M te steken die de overgang regelt van a,b,c,d,e naar $a_1,b_1,c_1,d_1,e_1$ . De overgang wordt geregeld door $A_1=M*A$ , hierbij is $A=(a,b,c,d,e)^t$ , $A_1=(a_1,b_1,c_1,d_1,e_1)^t$ en

$M= \begin{pmatrix}0&\frac{1}{3}&\frac{1}{3}&\frac{1}{3}&\frac{1}{3}\\\frac{1}{4}&0&\frac{1}{3}&0&\frac{1}{3}\\\frac{1}{4}&\frac{1}{3}&0&\frac{1}{3}&0\\\frac{1}{4}&0&\frac{1}{3}&0&\frac{1}{3}\\\frac{1}{4}&\frac{1}{3}&0&\frac{1}{3}&0\end{pmatrix}$

Het is duidelijk dat bij de vierde verplaatsing $A_4=M^4*A$ .

Berekening met een rekentoestel geeft:

$A_4=\begin{pmatrix}0,20987654\\0,21219136\\0,11342593\\0,21219136\\0,05555556\end{pmatrix}$

Er is dus ongeveer 5,56% kans dat de cavia zich na 4 verplaatsingen in kamer 5 zit.